【题目】观察探究,解决问题.在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H得到的四边形EFGH叫做中点四边形.
(1)如图1,求证:中点四边形EFGH是平行四边形;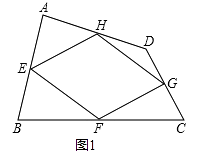
(2)请你探究并填空:
①当四边形ABCD变成平行四边形时,它的中点四边形是;
②当四边形ABCD变成矩形时,它的中点四边形是;
③当四边形ABCD变成正方形时,它的中点四边形是;
(3)如图2,当中点四边形EFGH为矩形时,对角线EG与FH相交于点O,P为EH上的动点,过点P作PM⊥EG,PN⊥FH,垂足分别为M、N,若EF=a,FG=b,请判断PM+PN的长是否为定值?若是,求出此定值;若不是,说明理由.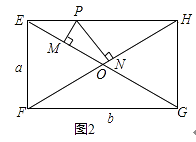
参考答案:
【答案】
(1)
解:连接AC,如图1,
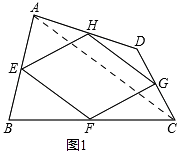
在△DAC中,HG∥AC,且HG= ![]() AC,
AC,
在△BAC中,EF∥AC,且EF= ![]() AC,
AC,
∴HG∥EF,且HG=EF,
∴四边形EFGH是平行四边形
(2)平行四边形;菱形;正方形
(3)
解:如图,
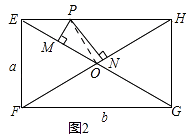
连接PO,
在矩形EFGH中:EO=HO= ![]() EG=
EG= ![]()
![]() ,
,
∵S△EOH= ![]() S四边形EFGH=
S四边形EFGH= ![]() ab=S△POE+S△POH,
ab=S△POE+S△POH,
∴ ![]() PM×EO+
PM×EO+ ![]() PN×HO=
PN×HO= ![]() ab,
ab,
∴ ![]()
![]() (PM+PN)=
(PM+PN)= ![]() ab,
ab,
∴PM+PN= ![]() .
.
故PM+PN是定值
【解析】解: (2)①在△DAC中,HG∥AC,且HG= ![]() AC,
AC,
在△BAC中,EF∥AC,且EF= ![]() AC,
AC,
∴HG∥EF,且HG=EF,
∴四边形EFGH是平行四边形.
所以答案是平行四边形,
②由(1)有,四边形EFGH是平行四边形.
同(1)的方法得,EH= ![]() BD,
BD,
∵四边形ABCD是矩形,
∴AC=BD
∴EH=EF,
∴平行四边形ABCD是菱形;
所以答案是菱形,
③由(2)②有,四边形EFGH是菱形.
∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠EFG=90°,
∴菱形ABCD是正方形;
所以答案是正方形,
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,

(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】若数轴上点A表示的数是1,则与点A距离为2的点所表示的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角
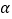 (
(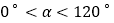 且
且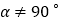 ),得到Rt△
),得到Rt△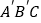 .
.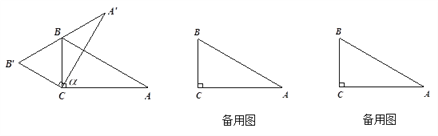
(1)如图,当边
 经过点B时,求旋转角
经过点B时,求旋转角 的度数;
的度数;(2)在三角板旋转的过程中,边
 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥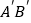 交
交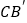 边于点E,联结BE.
边于点E,联结BE.①当
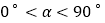 时,设AD=
时,设AD=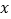 ,BE=
,BE=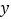 ,求
,求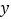 与
与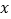 之间的函数解析式及自变量
之间的函数解析式及自变量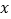 的取值范围;
的取值范围;②当
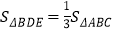 时,求AD的长.
时,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:

(1)∠1+∠2=90°;
(2)BE∥DF. -
科目: 来源: 题型:
查看答案和解析>>【题目】把一个正五边形绕它的中心旋转,至少旋转______度,就能与原来的位置重合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
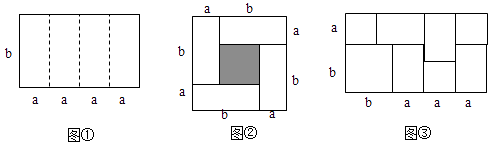
(1)图②中的阴影部分的面积为;
(2)观察图②请你写出 (a+b)2 , (a﹣b)2 , ab之间的等量关系是;
(3)根据(2)中的结论,若x+y=4,xy= ,则(x﹣y)2=;
,则(x﹣y)2=;
(4)实际上通过计算图形的面积可以探求相应的等式.如图③,你发现的等式是 .
相关试题

