【题目】为了认真贯彻教育部关于与开展“阳光体育”活动的文件精神,实施全国亿万学生每天集体锻炼一小时活动,吸引同学们走向操场、走进大自然、走到阳光下,积极参加体育锻炼,掀起校园内体育锻炼热潮,我市各学校结合实际情况举办了“阳光体育”系列活动,为了解“阳光体育”活动的落实情况,我市教育部门在红旗中学2000名学生中,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的活动),并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)参加调查的人数共有 人,在扇形统计图中,表示“C”的扇形的圆心角为 度;
(2)补全条形统计图,并计算扇形统计图中m的值;
(3)若要从该校喜欢“D”项目的学生中随机选择8名进行节目排练,则喜欢该项目的小丽同学被选中的概率是多少
参考答案:
【答案】(1)300,108;(2)图见解析,m=20;(3)![]() .
.
【解析】
试题分析:(1)用喜欢乒乓球的人数除以其所占的百分比即可求得调查的总人数,;(2)用喜欢C项目的人数除以总人数即可求得其百分率,从而得到m的值;(3)利用概率公式即可求得该同学被抽中的概率.
试题解析:(1)参加调查的人数为69÷23%=300(人),
∵“C”的人数为:300﹣60﹣69﹣36﹣45=90(人),
∴表示“C”的扇形的圆心角为![]() ×360°=108°,
×360°=108°,
(2)补全条形图如下:
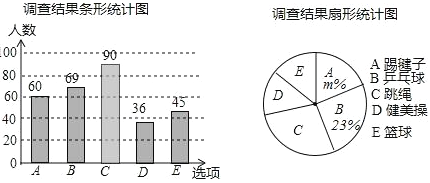
∵m%=![]() ×100%=20%,
×100%=20%,
∴m=20;
(3)![]() =
=![]() ,
,
答:喜欢该项目的小丽同学被选中的概率是![]() .
.
-
科目: 来源: 题型:
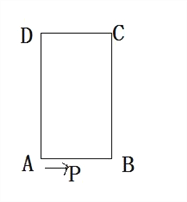
查看答案和解析>>【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒。
(1)当t=3秒时,求△ABP的面积;
(2)当t为何值时,点P与点A的距离为5cm?
(3)当t为何值时(2<t<5),以线段AD、CP、AP的长度为三角形是直角三角形,且AP是斜边。

-
科目: 来源: 题型:
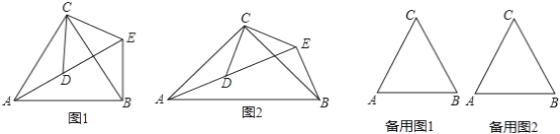
查看答案和解析>>【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.
填空:① ∠AEB的度数为_______;②线段AD、BE之间的数量关系是______.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
图1中的△ACB和△DCE,在△DCE旋转过程中当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某居民小区开展节约用电活动.该小区100户家庭4月份节电情况如图所示.那么四月份这100户家庭的节约电量,单位千瓦时的平均数是( )
节电量(千瓦时)
20
30
40
50
户数(户)
20
30
30
20
A.35B.26C.25D.20
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“若a,b互为倒数,则ab=1”的逆命题是___________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
第1个等式: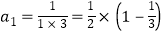 ; 第2个等式:
; 第2个等式: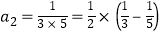 ;
;
第3个等式: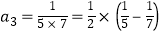 ; 第4个等式:
; 第4个等式: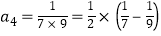 ;…
;…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= .
(2)用含有n的代数式表示第n个等式:an=(n为正整数)
(3)求a1+a2+a3+a4+…+a100的值.
(4)探究计算: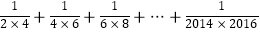
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下两组勾股数:11、 、 ; 13、 、 ;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别表示为 和 ,请用所学知识说明它们是一组勾股数.
相关试题

