【题目】点A在数轴上对应的数为a,点B对应的数为b,且a,b满足:|a+3|+(b-2)2=0
(1)求线段AB的长;
(2)如图①,点C在数轴上对应的数为x,且是方程![]() 的根,在数轴上是否存在点M使MA+MB=
的根,在数轴上是否存在点M使MA+MB=![]() BC+AB?若存在,求出点M对应的数;若不存在,说明理由;
BC+AB?若存在,求出点M对应的数;若不存在,说明理由;
(3)如图②,若N点是B点右侧一点,NA的中点为Q,P为NB的三等分点且靠近于B点,当N在B的右侧运动时,请直接判断![]() 的值是不变的还是变的,如果不变请直接写出其值,如果是变的请说明理由.
的值是不变的还是变的,如果不变请直接写出其值,如果是变的请说明理由.
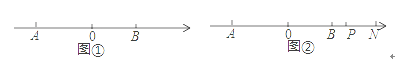
参考答案:
【答案】(1)线段AB的长为5;(2)存在,当点M表示的数为﹣5或4时,MA+MB=![]() BC+AB;(3)
BC+AB;(3)![]() 的值不变,为
的值不变,为![]() .
.
【解析】
(1)利用非负数的性质求出a与b的值,即可确定出AB的长;
(2)求出已知方程的解确定出x,得到C表示的点,设点M在数轴上对应的数是m,由MA+MB=![]() BC+AB确定出M位置,即可做出判断;
BC+AB确定出M位置,即可做出判断;
(3)设N点所表示的数为n,就有NA=n+3,NB=n﹣2,根据条件就可以表示出NQ=![]() NA=
NA=![]() ,BP=
,BP=![]() NB=
NB=![]() (n﹣2),再代入
(n﹣2),再代入![]() 求出其值即可.
求出其值即可.
(1)∵|a+3|+(b﹣2)2=0,
∴a+3=0,b﹣2=0,
∴a=﹣3,b=2,
∴AB=|﹣3﹣2|=5.
答:线段AB的长为5;
(2)存在,
∵x+1=![]() x﹣2,
x﹣2,
∴x=﹣6,
∴BC=8.
设点M在数轴上对应的数是m,
∵MA+MB=![]() BC+AB,
BC+AB,
∴|m+3|+|m﹣2|=![]() ×8+5,
×8+5,
令m+3=0,m﹣2=0,
∴m=﹣3或m=2.
①当m≤﹣3时,
﹣m﹣3+2﹣m=9, m=﹣5;
②当﹣3<m≤2时,
m+3+2﹣m=9(舍去);
③当m>2时,
m+3+m﹣2=9,
m=4.
∴当点M表示的数为﹣5或4时,MA+MB=![]() BC+AB;
BC+AB;
(3)设N点所表示的数为n,
∴NA=n+3,NB=n﹣2.
∵NA的中点为Q,
∴NQ=![]() NA=
NA=![]() ,
,
P为NB的三等分点且靠近于B点,
∴BP=![]() NB=
NB=![]() (n﹣2),
(n﹣2),
∴![]() ×
×![]() -
-![]() ×
×![]() (n-2)=
(n-2)=![]() ,
,
故![]() 的值是不变的.
的值是不变的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于
 EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则∠ADC的度数为 .
EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则∠ADC的度数为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为
 ,点B的坐标为
,点B的坐标为 ,点C在第一象限,对角线BD与x轴平行
,点C在第一象限,对角线BD与x轴平行 直线
直线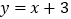 与x轴、y轴分别交于点E,
与x轴、y轴分别交于点E, 将菱形ABCD沿x轴向左平移m个单位,当点D落在
将菱形ABCD沿x轴向左平移m个单位,当点D落在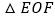 的内部时
的内部时 不包括三角形的边
不包括三角形的边 ,m的值可能是
,m的值可能是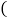

A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按下列方式搭建三角形:
 …
…(1)填表:
三角形个数
1
2
3
4
…
火柴棒根数
…
(2)当三角形的个数为n时,火柴棒的根数是多少?
(3)求当n=1 000时,火柴棒的根数是多少.
-
科目: 来源: 题型:
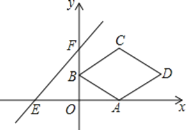
查看答案和解析>>【题目】如图,在△BC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.若使四边形ADCF是正方形,则应在△ABC中再添加一个条件为_____.
-
科目: 来源: 题型:
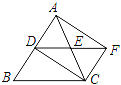
查看答案和解析>>【题目】在ABCD中,点E,F分别在边BC,AD上,且AF=CE.

(Ⅰ)如图①,求证四边形AECF是平行四边形;
(Ⅱ)如图②,若∠BAC=90°,且四边形AECF是边长为6的菱形,求BE的长.
-
科目: 来源: 题型:
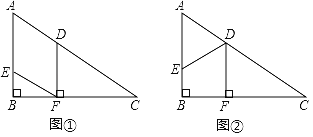
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒lcm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(I)试用含t的式子表示AE、AD、DF的长;
(Ⅱ)如图①,连接EF,求证:四边形AEFD是平行四边形;
(Ⅲ)如图②,连接DE,当t为何值时,四边形EBFD是矩形?并说明理由.
相关试题

