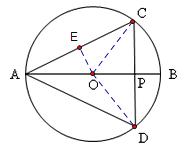
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AB=2,AC=![]() .
.
(1)求∠A的度数.
(2)求弧CBD的长.
(3)求弓形CBD的面积.

参考答案:
【答案】(1)∠A=30°;(2)![]() ;(3)
;(3)![]() -
-![]() .
.
【解析】试题分析:(1)过O作OE⊥AC,由垂径定理可得AE的长,再用三角函数即可求得∠A的度数;
(2)由∠A得度数得出对应圆心角∠COB的度数,由垂径定理得∠DOB=∠COB,由此得到∠COD的度数,用弧长公式即可求出弧长;
(3)由公式:弓形CBD的面积=扇形COD的面积△COD的面积,即可求出弓形面积.
试题解析:(1)过O作OE⊥AC,
![]() ,
,
![]()
在Rt△AEO中, ![]()
![]()
(2)连结OC,OD, ![]()
![]()
∵AB是⊙O的直径,弦CD⊥AB,
∴![]() =
=![]() ,
,
![]()
![]()
∵AB=2,
![]()
∴![]() 的长=
的长=![]() ;
;
(3) ![]() OP⊥CD,
OP⊥CD,
![]()
∵OC=1,
![]()
![]() ,
,
∴弓形CBD的面积=扇形COD的面积△COD的面积![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,计算下列五角星图案中五个顶角的度数和. 即:求∠A+∠B+∠C+∠D+∠E的大小.
(2)如图2,若五角星的五个顶角的度数相等, 求∠1的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,点D在AC上,点E在BA的延长线上,BD与CE相交于点F, 且BD=CE.

(1)求证:BF⊥CE.
(2)如图2,连结AF ,证明AF平分∠BFE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )


A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑全程的平均速度大于小林跑全程的平均速度
C. 小苏前15s跑过的路程大于小林前15s跑过的路程
D. 小林在跑最后100m的过程中,与小苏相遇2次
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为
 ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为

D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 经过某种变换后得到点
经过某种变换后得到点 ,我们把点
,我们把点
 叫做点
叫做点 的终结点.已知点
的终结点.已知点 的终结点为
的终结点为 ,点
,点 的终结点为
的终结点为 ,点
,点 的终结点为
的终结点为 ,这样依次得到
,这样依次得到 、
、 、
、 、
、 …
… ,若点
,若点 的坐标为
的坐标为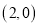 ,则点
,则点 的坐标为( )
的坐标为( )A.
 B.
B. C.
C.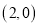 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地是一个降水丰富的地区,今年4月初,由于连续降雨导致该地某水库水位持续上涨,经观测水库1日—4日的水位变化情况,发现有这样规律, 1日,水库水位为
 米,此后日期每增加一天,水库水位就上涨
米,此后日期每增加一天,水库水位就上涨 米。
米。(1)请求出该水库水位
 (米)与日期
(米)与日期 (日)之间的函数表达式;(注:4月1日,即
(日)之间的函数表达式;(注:4月1日,即 ,4月2日,即
,4月2日,即 ,…,以次类推)
,…,以次类推)(2)请用求出的函数表达式预测该水库今年4月6日的水位.
相关试题

