【题目】如图,在矩形ABCD中,E是边AB的中点,连接DE,△ADE沿DE折叠后得到△FDE,点F在矩形ABCD的内部,延长DF交于BC于点G. 
(1)求证:FG=BG;
(2)若AB=6,BC=4,求DG的长.
参考答案:
【答案】
(1)证明:连接EG,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∵△ADE沿DE折叠后得到△FDE,
∴AE=EF,∠DFE=∠A=90°,
∴∠GFE=∠B,
∵E是边AB的中点,
∴AE=BE,
∴EF=EB,
在Rt△EFG与Rt△EBG中, ![]() ,
,
∴Rt△EFG≌Rt△EBG;
∴FG=BG
(2)解:∵AB=6,BC=4,△ADE沿DE折叠后得到△FDE,
∴DF=DA=4,EF=AE=3,∠AED=∠FED,
∵Rt△EFG≌Rt△EBG,
∴∠FEG=∠BEG,
∴∠DEF+∠FEG=90°,
∵EF⊥DG,
∴EF2=DFFG,
∴FG= ![]() ,
,
∴DG=FG+DF= ![]() .
.

【解析】(1)连接EG,根据矩形的性质得到∠A=∠B=90°,根据折叠的性质得到AE=EF,∠DFE=∠A=90°,根据全等三角形的性质即可得到结论;(2)根据折叠的性质得到DF=DA=4,EF=AE=3,∠AED=∠FED,根据全等三角形的性质得到∠FEG=∠BEG,得到∠DEF+∠FEG=90°,根据射影定理即可得到结论.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=45°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,连接P1P2交OA、OB于E、F,若P1E=
 ,OP=
,OP=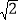 ,则EF的长度是_____.
,则EF的长度是_____.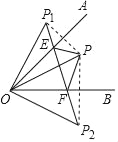
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为﹣10和6,动点P从点A出发,以每秒6个单位长度的速度沿数轴正方向匀速运动,同时动点Q从点B出发,以每秒3个单位的速度沿数轴负方向匀速运动,设运动时间为t(t>0)秒
(1)当t=2时,求AP的中点C所对应的数;
(2)当PQ=OA时,求点Q所对应的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】家庭过期药品属于“国家危险废物“处理不当将污染环境,危害健康.某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图:
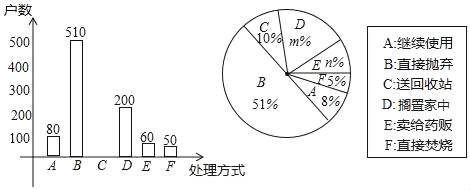
(1)求m、n的值;
(2)补全条形统计图;
(3)家庭过期药品的正确处理方式是送回收站,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区计划对面积为400m2的区域进行绿化.经测算,甲队每天能完成绿化面积是乙队每天能完成绿化面积的2倍,且甲队单独完成比乙队单独完成少用4天.求甲、乙两队每天单独完成绿化的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为6,点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒4个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,请求出所有满足条件的t值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4cm,动点P以1cm/s的速度分别从点A、B同时出发,点P沿A→B向终点B运动,点Q沿B→A向终点A运动,过点P作PD⊥AC于点D,以PD为边向右侧作正方形PDEF,过点Q作QG⊥AB,交折线BC﹣CA于点G与点C不重合,以QG为边作等腰直角△QGH,且点G为直角顶点,点C、H始终在QG的同侧,设正方形PDEF与△QGH重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<4).
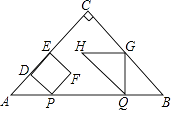
(1)当点F在边QH上时,求t的值;
(2)当正方形PDEF与△QGH重叠部分图形是四边形时,求S与t之间的函数关系式;
(3)当FH所在的直线平行或垂直于AB时,直接写出t的值.
相关试题

