【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为﹣10和6,动点P从点A出发,以每秒6个单位长度的速度沿数轴正方向匀速运动,同时动点Q从点B出发,以每秒3个单位的速度沿数轴负方向匀速运动,设运动时间为t(t>0)秒
(1)当t=2时,求AP的中点C所对应的数;
(2)当PQ=OA时,求点Q所对应的数.

参考答案:
【答案】(1)AP的中点C所对应的数为﹣4;(2)点Q所对应的数为4或﹣![]() .
.
【解析】
(1)先求出t=2时P点对应的数,再根据中点坐标公式求解即可;
(2)设运动时间为t(t>0)秒时,PQ=OA=10.求出P、Q两点对应的数.分两种情况进行讨论:①相遇前;②相遇后.
(1)当t=2时,P点对应的数为﹣10+6×2=2,
∵数轴上点A所表示的数为﹣10,
∴AP的中点C所对应的数为![]() =﹣4;
=﹣4;
(2)设运动时间为t(t>0)秒时,PQ=OA=10.
此时,P点对应的数为﹣10+6t,Q点对应的数为6﹣3t.
①相遇前,由题意,得6﹣3t﹣(﹣10+6t)=10,解得t=![]() ,
,
此时,Q点对应的数为6﹣3t=6﹣3×![]() =4;
=4;
②相遇后,由题意,得﹣10+6t﹣(6﹣3t)=10,解得t=![]() ,
,
此时,Q点对应的数为6﹣3t=6﹣3×![]() =﹣
=﹣![]() .
.
综上可知,点Q所对应的数为4或﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y1=ax2+bx过(﹣2,4),(﹣4,4)两点.
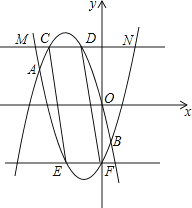
(1)求二次函数y1的解析式;
(2)将y1沿x轴翻折,再向右平移2个单位,得到抛物线y2 , 直线y=m(m>0)交y2于M、N两点,求线段MN的长度(用含m的代数式表示);
(3)在(2)的条件下,y1、y2交于A、B两点,如果直线y=m与y1、y2的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与y1、y2的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,延长△ABC的各边,使得BF=AC,AE=CD=AB,连结DE,EF,FD,得到△DEF为等边三角形.
求证:(1)△AEF≌△CDE;
(2)△ABC为等边三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
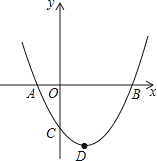
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.当a= 时,△ABD是等腰直角三角形
时,△ABD是等腰直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
(1)如图①.当∠COD在∠AOB的内部时
①若∠AOC=39°40′,求∠DOE的度数;
②若∠AOC=α,求∠DOE的度数(用含α的代数式表示),
(2)如图②,当∠COD在∠AOB的外部时,
①请直接写出∠AOC与∠DOE的度数之间的关系;
②在∠AOC内部有一条射线OF,满足∠AOC+2∠BOE=4∠AOF,写出∠AOF与∠DOE的度数之间的关系.
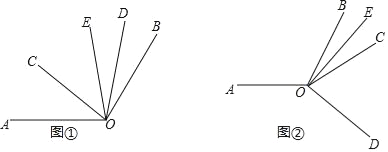
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形中,两条直角边的长度分别为a和b,斜边长度为c,则a2+b2=c2,即两条直角边的平方和等于斜边的平方,此结论称为勾股定理.在一张纸上画两个同样大小的直角三角形ABC和A′B′C′,并把它们拼成如图所示的形状 (点C和A′重合,且两直角三角形的斜边互相垂直).请利用拼得的图形证明勾股定理.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠C=2∠B,D是BC边上的一点,且AD⊥AB,E是BD的中点,连结AE.
求证:(1)∠AEC=∠C;
(2)BD=2AC.

相关试题

