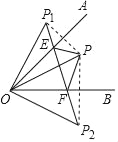
【题目】已知∠AOB=45°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,连接P1P2交OA、OB于E、F,若P1E=![]() ,OP=
,OP=![]() ,则EF的长度是_____.
,则EF的长度是_____.
参考答案:
【答案】![]()
【解析】
由P,P1关于直线OA对称,P、P2关于直线OB对称,推出OP=OP1=OP2,∠AOP=∠AOP1,∠BOP=∠BOP2,推出∠P1OP2=90°,由此即可判断△P1OP2是等腰直角三角形,由轴对称可得,∠OPE=∠OP1E=45°,∠OPF=∠OP2F=45°,进而得出∠EPF=90°,最后依据勾股定理列方程,即可得到EF的长度.
∵P,P1关于直线OA对称,P、P2关于直线OB对称,
∴OP=OP1=OP2=![]() ,∠AOP=∠AOP1,∠BOP=∠BOP2,
,∠AOP=∠AOP1,∠BOP=∠BOP2,
∵∠AOB=45°,
∴∠P1OP2=2∠AOP+2∠BOP=2(∠AOP+∠BOP)=90°,
∴△P1OP2是等腰直角三角形,
∴P1P2=![]() =2,
=2,
设EF=x,
∵P1E=![]() =PE,
=PE,
∴PF=P2F=![]() -x,
-x,
由轴对称可得,∠OPE=∠OP1E=45°,∠OPF=∠OP2F=45°,
∴∠EPF=90°,
∴PE2+PF2=EF2,即(![]() )2+(
)2+(![]() -x)2=x2,
-x)2=x2,
解得x=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=4,DE=7,则线段EC的长为( )

A. 3 B. 4 C. 3.5 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=
 的图象与一次函数y=ax+b的图象交于点A(﹣2,3)和点B(m,﹣2).
的图象与一次函数y=ax+b的图象交于点A(﹣2,3)和点B(m,﹣2).
(1)求反比例函数和一次函数的解析式;
(2)直线x=1上有一点P,反比例函数图象上有一点Q,若以A、B、P、Q为顶点的四边形是以AB为边的平行四边形,直接写出点Q的坐标. -
科目: 来源: 题型:
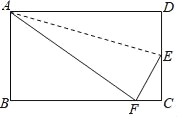
查看答案和解析>>【题目】如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.已知AB=3cm,BC=5cm.则EC的长为_____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为﹣10和6,动点P从点A出发,以每秒6个单位长度的速度沿数轴正方向匀速运动,同时动点Q从点B出发,以每秒3个单位的速度沿数轴负方向匀速运动,设运动时间为t(t>0)秒
(1)当t=2时,求AP的中点C所对应的数;
(2)当PQ=OA时,求点Q所对应的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】家庭过期药品属于“国家危险废物“处理不当将污染环境,危害健康.某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图:
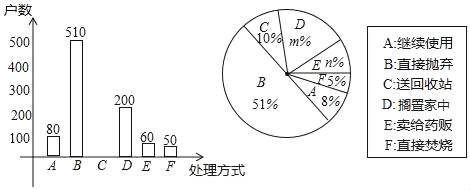
(1)求m、n的值;
(2)补全条形统计图;
(3)家庭过期药品的正确处理方式是送回收站,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是边AB的中点,连接DE,△ADE沿DE折叠后得到△FDE,点F在矩形ABCD的内部,延长DF交于BC于点G.

(1)求证:FG=BG;
(2)若AB=6,BC=4,求DG的长.
相关试题

