【题目】已知:如图,∠MON在∠AOB的内部,点C、D分别在射线OA、OB上,且OC=OD,CE⊥OA,DF⊥OB,分别交OM、ON于点E,F.
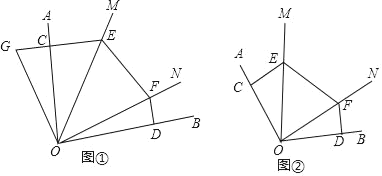
(1)如图①所示,若∠AOB=90°,∠MON=45°,延长EC至点G,使得CG=DF.请证明EF=CE+DF;
(2)如图②所示,若∠AOB=115°,EF=CE+DF,求∠MON的度数?
参考答案:
【答案】(1)详见解析;(2)∠MON=57.5°
【解析】
(1)先证出△OCG≌△ODF(SAS),再证出△EOG≌△EOF(SAS),即可得:EF=CE+DF;
(2)仿照(1)的思路,延长EC至G,使CG=DF,连接OG,先证明:△OCG≌△ODF(SAS),再证明:△OEG≌△OEF(SSS),即可求得:∠MON=57.5°.
解:(1)如图①,
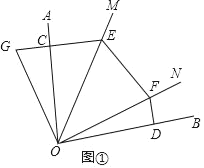
证明:∵CE⊥OA,DF⊥OB,
∴∠OCG=∠ODF=90°,
∵OC=OD,CG=DF.
∴△OCG≌△ODF(SAS)
∴∠COG=∠DOF,OG=OF
∵∠AOB=90°,∠MON=45°,
∴∠COE+∠DOF=45°
∴∠COE+∠COG=45°
即∠EOG=45°=∠MON
在△EOG≌△EOF中
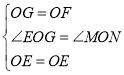
∴△EOG≌△EOF(SAS)
∴EF=EG
即:EF=CE+DF.
(2)如图②,延长EC至G,使CG=DF,连接OG,
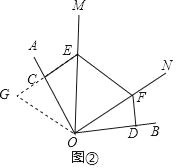
∵CE⊥OA,DF⊥OB,
∴∠OCG=∠ODF=90°,
∵OC=OD,CG=DF.
∴△OCG≌△ODF(SAS)
∴∠COG=∠DOF,OG=OF
∵EG=CE+CG=CE+DF,EF=CE+DF,
∴EG=EF
∵OE=OE
∴△OEG≌△OEF(SSS)
∴∠EOG=∠EOF
∵∠EOG+∠EOF=∠COG+∠AOF=∠DOF+∠AOF=∠AOB=115°
∴∠EOF=![]() ∠AOB=57.5°
∠AOB=57.5°
即:∠MON=57.5°
-
科目: 来源: 题型:
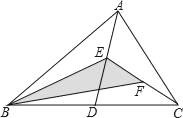
查看答案和解析>>【题目】如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,若△ABC的面积为16,则图中阴影部分的面积为_____.
-
科目: 来源: 题型:
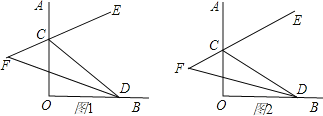
查看答案和解析>>【题目】如图,∠AOB=90°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.
(1)当∠OCD=50°(图1),试求∠F.
(2)当C、D在射线OA、OB上任意移动时(不与点O重合)(图2),∠F的大小是否变化?若变化,请说明理由;若不变化,求出∠F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
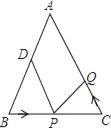
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E,连接BD,DE,若∠A=30°,AB=AC,则∠BDE的度数为( ).

A.52.5°B.60°C.67.5°D.75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为________度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解本校2400名学生对某次足球赛的关注程度,以利于做好教育和引导工作,随机抽取了本校内的六、七、八、九四个年级部分学生进行调查,按“各年级被抽取人数”与“关注程度”,分别绘制了条形统计图(图①)、扇形统计图(图②)和折线统计图(图③).

(1)本次共随机抽查了________名学生,根据信息补全图①中条形统计图,图②中八年级所对应扇形的圆心角的度数为________;
(2)如果把“特别关注”“一般关注”“偶尔关注”都看成关注,那么全校关注足球赛的学生大约有多少名?
(3)①根据上面的统计结果,谈谈你对该校学生对足球关注的现状的看法及建议;
②如果要了解中小学生对校园足球的关注情况,你认为应该如何进行抽样?
相关试题

