【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
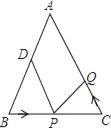
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
参考答案:
【答案】(1)详见解析;(2)点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为![]() cm/s时,能够使△BPD与△CQP全等.
cm/s时,能够使△BPD与△CQP全等.
【解析】
(1)经过1秒后,PB=3cm,PC=5cm,CQ=3cm,由已知可得BD=PC,BP=CQ,∠ABC=∠ACB,即据SAS可证得△BPD≌△CQP.
(2)可设点Q的运动速度为x(x≠3)cm/s,经过ts △BPD与△CQP全等,则可知PB=3t cm,PC=(8-3t)cm,CQ=xt cm,据(1)同理可得当BD=PC,BP=CQ或BD=CQ,BP=PC时两三角形全等,求x的解即可.
解:(1)经过1秒后,PB=3cm,PC=5cm, CQ=3cm,
∵△ABC中,AB=AC,
∴在△BPD和△CQP中,
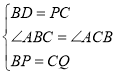 ,
,
∴△BPD≌△CQP(SAS).
(2)设点Q的运动速度为x(x≠3)cm/s,经过ts△BPD与△CQP全等;则可知PB=3t cm,PC=(8-3t)cm,CQ=xt cm,
∵AB=AC,
∴∠B=∠C,
根据全等三角形的判定定理SAS可知,有两种情况:
①当BD=PC,BP=CQ时,②当BD=CQ,BP=PC时,两三角形全等;
①当BD=PC且BP=CQ时,
8﹣3t=5且3t=xt,解得x=3,
∵x≠3,
∴舍去此情况;
②BD=CQ,BP=PC时,
5=xt且3t=8﹣3t,
解得:x=![]() ;
;
故若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为![]() cm/s时,能够使△BPD与△CQP全等.
cm/s时,能够使△BPD与△CQP全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,若分别以△ABC的AC、BC两边为边向外侧作的四边形ACDE和BCFG为正方形,则称这两个正方形为外展双叶正方形.
(1)发现:如图2,当∠C=90°时,求证:△ABC与△DCF的面积相等.
(2)引申:如果∠C
 90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;
90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;(3)运用:如图3,分别以△ABC的三边为边向外侧作的四边形ACDE、BCFG和ABMN为正方形,则称这三个正方形为外展三叶正方形.已知△ABC中,AC=3,BC=4.当∠C=_____°时,图中阴影部分的面积和有最大值是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,若△ABC的面积为16,则图中阴影部分的面积为_____.
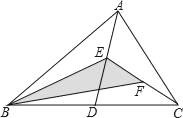
-
科目: 来源: 题型:
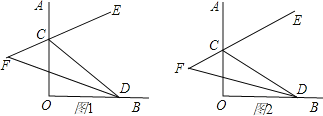
查看答案和解析>>【题目】如图,∠AOB=90°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.
(1)当∠OCD=50°(图1),试求∠F.
(2)当C、D在射线OA、OB上任意移动时(不与点O重合)(图2),∠F的大小是否变化?若变化,请说明理由;若不变化,求出∠F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠MON在∠AOB的内部,点C、D分别在射线OA、OB上,且OC=OD,CE⊥OA,DF⊥OB,分别交OM、ON于点E,F.
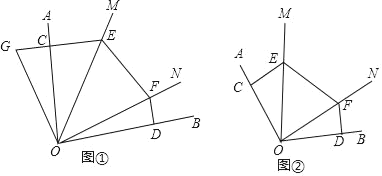
(1)如图①所示,若∠AOB=90°,∠MON=45°,延长EC至点G,使得CG=DF.请证明EF=CE+DF;
(2)如图②所示,若∠AOB=115°,EF=CE+DF,求∠MON的度数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E,连接BD,DE,若∠A=30°,AB=AC,则∠BDE的度数为( ).

A.52.5°B.60°C.67.5°D.75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为________度.

相关试题

