【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=4cm,∠CAB=60°,P是弧 ![]() 上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是 .
上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是 . 
参考答案:
【答案】( ![]() ﹣1)cm
﹣1)cm
【解析】解:如图,以AC为直径作圆O′,连接BO′、BC. 
∵CD⊥AP,
∴∠ADC=90°,
∴在点P移动的过程中,点D在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AB=4cm,∠CAB=60°,
∴BC=ABsin60°=2 ![]() ,AC=ABcos60°=2cm.
,AC=ABcos60°=2cm.
在Rt△BCO′中,BO′= ![]() =
= ![]() =
= ![]() ,
,
∵O′D+BD≥O′B,
∴当O′、D、B共线时,BD的值最小,最小值为O′B﹣O′D= ![]() ﹣1,
﹣1,
所以答案是( ![]() ﹣1)cm.
﹣1)cm.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半).
-
科目: 来源: 题型:
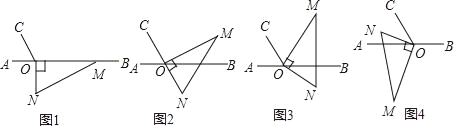
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至图2,使点N在OC的反向延长线上,请直接写出图中∠MOB的度数;
(2)将图1中的三角尺绕点O逆时针旋转至图3,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;
(3)将图1中的三角尺绕点O顺时针旋转至图4,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A、B、C,完成下列问题:

(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E为BA的中点(E到A、C两点的距离相等),井在数轴上标出点E表示的数,求出CE的长.
(3)O为原点,取OC的中点M,分OC分为两段,记为第一次操作:取这两段OM、CM的中点分别为了N1、N2,将OC分为4段,记为第二次操作,再取这两段的中点将OC分为8段,记为第三次操作,第六次操作后,OC之间共有多少个点?求出这些点所表示的数的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )
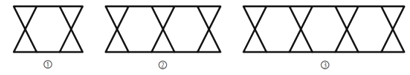
A. 12 B. 14 C. 16 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简:
(1)计算:2﹣1+ cos30°+|﹣5|﹣(π﹣2017)0
cos30°+|﹣5|﹣(π﹣2017)0
(2)化简:(x﹣5+ )÷
)÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.
(1)请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)若我市初中生共有16000人,竞赛活动获奖率为40%,获三等奖以上的学生表示对“足球比较喜欢”,请你估计我市初中生对“足球比较喜欢”的有多少人?
相关试题

