【题目】已知反比例函数![]() (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
参考答案:
【答案】(1)![]() ;(2)点B不在该函数图象上|点C在该函数图象上;(3)-6<y<-2.
;(2)点B不在该函数图象上|点C在该函数图象上;(3)-6<y<-2.
【解析】试题分析:(1)把点A的坐标代入已知函数解析式,通过方程即可求得k的值.
(2)只要把点B、C的坐标分别代入函数解析式,横纵坐标坐标之积等于6时,即该点在函数图象上;
(3)根据反比例函数图象的增减性解答问题.
试题解析:(1)∵反比例函数y=![]() (k为常数,k≠0)的图象经过点A(2,3),
(k为常数,k≠0)的图象经过点A(2,3),
∴把点A的坐标代入解析式,得
3=![]() ,
,
解得,k=6,
∴这个函数的解析式为:y=![]() ;
;
(2)∵反比例函数解析式y=![]() ,
,
∴6=xy.
分别把点B、C的坐标代入,得
(-1)×6=-6≠6,则点B不在该函数图象上.
3×2=6,则点C在该函数图象上;
(3)∵当x=-3时,y=-2,当x=-1时,y=-6,
又∵k>0,
∴当x<0时,y随x的增大而减小,
∴当-3<x<-1时,-6<y<-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);
②g(m,n)=(﹣m,﹣n),如g (2,1)=(﹣2,﹣1)
按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据3,a,4,5的众数为4,则这组数据的平均数为( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x2=5x+2的二次项系数为_____,一次项系数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC水平向右平移5个单位得到△A′B′C′.
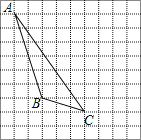
(1)补全△A′B′C′;利用网格点和直尺画图:
(2)画出AB边上的高线CD;
(3)图中△ABC的面积是 ;
(4)△ABC与△EBC面积相等,在图中描出所有满足条件且异于A点的格点E,并记为E1E2E3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在山顶上有一座电视塔,在塔顶B处,测得地面上一点A的俯角α=60°,在塔底C处测得的俯角β=45°,已知BC=60m,求山高CD(精确到1m,
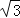 ≈1.732)
≈1.732)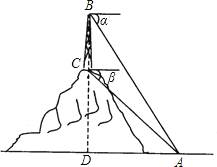
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣4x+2=0的两根为x1,x2,则x12﹣4x1+2x1x2的值为_____.
相关试题

