【题目】已知:如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,
(1)若∠BDO=∠CEO,求证:BE=CD.
(2)若点E为AC中点,问点D满足什么条件时候,![]() .
.

参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】分析:
(1)由AB=AC可得∠ABC=∠ACB,结合∠BDO=∠CEO和BC=CB可得△DBC≌△ECB,由此可得BE=CD;
(2)由E为AC中点可知,若此时D为AB的中点,则由三角形中位线定理可得DE∥BC,DE=![]() BC,从而可得△DEO∽△BCO,由此即可得到
BC,从而可得△DEO∽△BCO,由此即可得到![]() .
.
详解:
(1)∵AB=AC,
∴∠ABC=∠ACB,
在△DBC与△ECB中, ,
,
∴△DBC≌△ECB,
∴BE=CD;
(2)当点D为AB的中点时,![]() ,理由如下:
,理由如下:
∵点E为AC中点,点D为AB的中点,
∴DE=![]() BC,DE∥BC,
BC,DE∥BC,
∴△DEO∽△BCO,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若多项式2x3﹣8x2y+x+1与多项式﹣3x3﹣2mx2y+6x﹣9的差的值与字母y的取值无关,求m的值.
(2)已知有理数a,b,c在数轴上对应位置如图所示,化简:|a+b|﹣|b+c|+|a+c|.
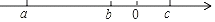
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内划出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:

依此估计此封闭图形ABC的面积是_____m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴按下图中的方式搭图形:

(1)按图示规律补全表格:
图形编号
①
②
③
④
⑤
火柴棒根数
7
12
(2)按照这种方式搭下去,请写出搭第n个图形需要的火柴根数;
(3)小明发现:按照这种方式搭图形会产生若干个正方形,若使用187根火柴搭图形,图中会产生多少个正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上两点A,B表示的数分别为﹣2,6,用符号“AB”来表示点A和点B之间的距离.

(1)求AB的值;
(2)若在数轴上存在一点C,使AC=3BC,求点C表示的数;
(3)在(2)的条件下,点C位于A、B两点之间.点A以1个单位/秒的速度沿着数轴的正方向运动,2秒后点C以2个单位/秒的速度也沿着数轴的正方向运动,到达B点处立刻返回沿着数轴的负方向运动,直到点A到达点B,两个点同时停止运动.设点A运动的时间为t,在此过程中存在t使得AC=3BC仍成立,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产某产品100吨,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为“+”,减少的吨数记为“﹣”)
星期
一
二
三
四
五
六
日
增减/吨
﹣1
+3
﹣2
+4
+7
﹣7
﹣11
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t)
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.

相关试题

