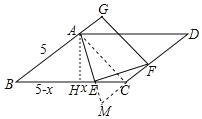
【题目】如图,ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,延长BA到点G,使AG=CF,连接GF,若BC=7,DF=3,AE=![]() ,则GF的长为__________
,则GF的长为__________

参考答案:
【答案】3![]() .
.
【解析】
首先延长AE、DC相交于点M,过点A作AH⊥BC于点H,连接AC,进而得出FC的长,再利用勾股定理得出EH的长,即可得出FG的长
延长AE、DC相交于点M,过点A作AH⊥BC于点H,连接AC,
∵AB∥DM,
∴∠M=∠BAE,∠CEM=∠DAM,
而∠BAE=∠DAM,
∴∠M=∠CEM=∠DAM,
∴CE=CM,DM=AD=7,
∵∠M+∠MFE=90°=∠CEM+∠CEF,
∴∠MFE=∠CEF,
∴CF=CE=CM=![]() FM=
FM=![]() (MD-DF)=2,
(MD-DF)=2,
∴AB=DC=DF+CF=5,BE=BC-CE=5,
设EH=x,可得:BH=5-x,
∵AH2=AE2-EH2=AB2-BE2,
∴10-x2=25-(5-x)2
解得:x=1,
则EH=1,AH=3,
故CH=CE+EH=3,
则AC=![]() =3
=3![]() ,
,
而四边形ACFG是平行四边形,
故FG=AC=3![]() .
.
故答案为:3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是矩形ABCD对角线的交点,DE平分∠ADC交BC于点E,若∠BDE=15°,则∠COE=_______度

-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,若∠BAD与∠ABC的角平分线分别交CD于点E,F,且AD=2EF=2,则AB=___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在图一中,将等边
 绕BC边中点D顺时针旋转
绕BC边中点D顺时针旋转 至
至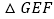 ,直线AG与直线CF交于点
,直线AG与直线CF交于点 求证
求证 .小明同学的思路是这样的:通过证明
.小明同学的思路是这样的:通过证明 ∽
∽ 得到
得到 ,从而得到
,从而得到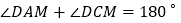 ,继续推理就可以使问题得到解决.
,继续推理就可以使问题得到解决. 请根据小明的思路,求证:
请根据小明的思路,求证: ;
; 爱动脑筋的小明把问题做了进一步思考,他想:如果把题目的“等边
爱动脑筋的小明把问题做了进一步思考,他想:如果把题目的“等边 ”改成“等腰直角
”改成“等腰直角 ,其中
,其中 ,
, ”,如图二,
”,如图二, 中的结论还成立吗?如果成立,求此时线段BM的最大值.
中的结论还成立吗?如果成立,求此时线段BM的最大值. 小明继续大胆设问:如图三,在
小明继续大胆设问:如图三,在 中,
中, ,
, ,将这样的
,将这样的 按照题目中的方式旋转
按照题目中的方式旋转 ,请直接写出AG与CF的位置关系以及线段BM的变化范围.
,请直接写出AG与CF的位置关系以及线段BM的变化范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,指针分别指向红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.
(1)分别计算获一、二、三等奖的概率.
(2)老李一次性购物满了300元,摇奖一次,获奖的概率是多少?请你预测一下老李摇奖结果会有哪几种情况?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCO的两边OA、OC在坐标轴的正半轴上,
 轴,
轴, ,以直线
,以直线 为对称轴的抛物线过A,B,C三点.
为对称轴的抛物线过A,B,C三点. 求该抛物线的函数解析式;
求该抛物线的函数解析式; 已知抛物线交x轴的负半轴于点D,直线BD交y轴于点N,点
已知抛物线交x轴的负半轴于点D,直线BD交y轴于点N,点 是线段AD上一个动点,过点E作x轴的垂线交直线BD于点P,交抛物线于点F,求当
是线段AD上一个动点,过点E作x轴的垂线交直线BD于点P,交抛物线于点F,求当 时相应的m的值.
时相应的m的值. 在
在 的条件下,连接CP以CP为一边向外作正方形CPGH,如图2所示,当正方形的顶点G或顶点H随着点E的运动落在抛物线上时,直接写出此时点E的坐标.
的条件下,连接CP以CP为一边向外作正方形CPGH,如图2所示,当正方形的顶点G或顶点H随着点E的运动落在抛物线上时,直接写出此时点E的坐标.
相关试题

