【题目】如图,四边形ABCO的两边OA、OC在坐标轴的正半轴上,![]() 轴,
轴,![]() ,以直线
,以直线![]() 为对称轴的抛物线过A,B,C三点.
为对称轴的抛物线过A,B,C三点.
![]() 求该抛物线的函数解析式;
求该抛物线的函数解析式;
![]() 已知抛物线交x轴的负半轴于点D,直线BD交y轴于点N,点
已知抛物线交x轴的负半轴于点D,直线BD交y轴于点N,点![]() 是线段AD上一个动点,过点E作x轴的垂线交直线BD于点P,交抛物线于点F,求当
是线段AD上一个动点,过点E作x轴的垂线交直线BD于点P,交抛物线于点F,求当![]() 时相应的m的值.
时相应的m的值.
![]() 在
在![]() 的条件下,连接CP以CP为一边向外作正方形CPGH,如图2所示,当正方形的顶点G或顶点H随着点E的运动落在抛物线上时,直接写出此时点E的坐标.
的条件下,连接CP以CP为一边向外作正方形CPGH,如图2所示,当正方形的顶点G或顶点H随着点E的运动落在抛物线上时,直接写出此时点E的坐标.

参考答案:
【答案】(1)![]() ;(2)m的值为
;(2)m的值为![]() 或
或![]() ;(3)
;(3)![]() 点坐标为
点坐标为![]() ,
,![]() .
.
【解析】
![]() 由待定系数法,求解析式;
由待定系数法,求解析式;
![]() 求出BD解析式,用m表示点P坐标,及PF,由
求出BD解析式,用m表示点P坐标,及PF,由![]() 可知
可知![]() ,求m即可
,求m即可
![]() 用m表示H、G坐标,可以找到G、H运动过程中所在函数解析式,表示这两个解析式,分别求其与抛物线交点,再求m即可.
用m表示H、G坐标,可以找到G、H运动过程中所在函数解析式,表示这两个解析式,分别求其与抛物线交点,再求m即可.
解:![]() ,
,
![]() ,
,![]() ,
,
![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]() ,
,
![]() ,
,
设抛物线解析式为![]() ,
,
把![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ,
,
即![]() ;
;
![]() 如图1,
如图1,

![]() 轴,
轴,
![]() 点与C点关于直线
点与C点关于直线![]() 对称,
对称,
![]() ,
,
设直线BD的解析式为![]() ,
,
把![]() ,
,![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
![]() 直线BD的解析式为
直线BD的解析式为![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
点E坐标为![]() ,则
,则![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
解方程![]() 得
得![]() ,
,![]() 舍去
舍去![]() ,
,
解方程![]() 得
得![]() ,
,![]() ,
,
综上所述,m的值为![]() 或
或![]() ;
;
![]() 作
作![]() 轴于K,
轴于K,![]() 轴于L,如图3,
轴于L,如图3,
![]() 四边形PCGH为正方形,
四边形PCGH为正方形,
![]() ,
,![]() ,
,
易得![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,G点纵坐标为
,G点纵坐标为![]() ,
,
设点H横坐标![]() ,
,![]() ,
,
则点H在直线![]() 上,
上,
![]() ,
,
解得
![]() 或
或![]() ,
,
![]() 或
或![]()
![]() 点纵坐标为2
点纵坐标为2
![]() ,
,
解得![]()
![]() 当
当![]() 时,
时,![]() ,
,
解得![]() .
.
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,延长BA到点G,使AG=CF,连接GF,若BC=7,DF=3,AE=
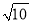 ,则GF的长为__________
,则GF的长为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在图一中,将等边
 绕BC边中点D顺时针旋转
绕BC边中点D顺时针旋转 至
至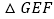 ,直线AG与直线CF交于点
,直线AG与直线CF交于点 求证
求证 .小明同学的思路是这样的:通过证明
.小明同学的思路是这样的:通过证明 ∽
∽ 得到
得到 ,从而得到
,从而得到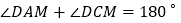 ,继续推理就可以使问题得到解决.
,继续推理就可以使问题得到解决. 请根据小明的思路,求证:
请根据小明的思路,求证: ;
; 爱动脑筋的小明把问题做了进一步思考,他想:如果把题目的“等边
爱动脑筋的小明把问题做了进一步思考,他想:如果把题目的“等边 ”改成“等腰直角
”改成“等腰直角 ,其中
,其中 ,
, ”,如图二,
”,如图二, 中的结论还成立吗?如果成立,求此时线段BM的最大值.
中的结论还成立吗?如果成立,求此时线段BM的最大值. 小明继续大胆设问:如图三,在
小明继续大胆设问:如图三,在 中,
中, ,
, ,将这样的
,将这样的 按照题目中的方式旋转
按照题目中的方式旋转 ,请直接写出AG与CF的位置关系以及线段BM的变化范围.
,请直接写出AG与CF的位置关系以及线段BM的变化范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,指针分别指向红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.
(1)分别计算获一、二、三等奖的概率.
(2)老李一次性购物满了300元,摇奖一次,获奖的概率是多少?请你预测一下老李摇奖结果会有哪几种情况?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船位于灯塔B的正西方向A处,且A处与灯塔B相距60海里,轮船沿东北方向匀速航行,到达位于灯塔B的北偏东l5°方向上的C处.

(1)求∠ACB的度数;
(2)求灯塔B到C处的距离.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC

①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】农夫将苹果树种在正方形的果园内,为了保护苹果树不受风吹,他在苹果树的周围种上针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )

A. 6 B. 8 C. 12 D. 16
相关试题

