【题目】在ABCD中,若∠BAD与∠ABC的角平分线分别交CD于点E,F,且AD=2EF=2,则AB=___.
参考答案:
【答案】3或5.
【解析】
AE与BF相交,由于平行四边形的两组对边互相平行,又AE平分∠BAD,由此可以推出所以∠BAE=∠DAE,则DE=AD=2;同理可得,CF=CB=2,而EF=CF+DE-DC,由此可以求出AB长.
AE与BF不相交,由于平行四边形的两组对边互相平行,又AE平分∠BAD,由此可以推出所以∠BAE=∠DAE,则DE=AD=2;同理可得,CF=CB=2,而EF=DC-(DE+CF),由此可以求出AB长.
AE与BF相交,如图所示:∵AE平分∠BAD,

∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠EAB=∠DEA,
∴∠DAE=∠AED,
则AD=DE=2;
同理可得,CF=CB=2.
∵EF=DE+CF-DC=2+2-CD=1.
∴AB=DC=3;
AE与BF不相交,如图所示:∵AE平分∠BAD,

∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠EAB=∠DEA,
∴∠DAE=∠AED,
则AD=DE=2;
同理可得,CF=CB=2.
∵EF=DC-(DE+CF)=CD-(2+2)=1.
∴AB=DC=5.
故答案为:3或5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵
 两次共花费940元
两次共花费940元 两次购进的A、B两种花草价格均分别相同
两次购进的A、B两种花草价格均分别相同 .
. 、B两种花草每棵的价格分别是多少元?
、B两种花草每棵的价格分别是多少元? 若再次购买A、B两种花草共12棵
若再次购买A、B两种花草共12棵 、B两种花草价格不变
、B两种花草价格不变 ,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是矩形ABCD对角线的交点,DE平分∠ADC交BC于点E,若∠BDE=15°,则∠COE=_______度

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,延长BA到点G,使AG=CF,连接GF,若BC=7,DF=3,AE=
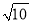 ,则GF的长为__________
,则GF的长为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在图一中,将等边
 绕BC边中点D顺时针旋转
绕BC边中点D顺时针旋转 至
至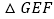 ,直线AG与直线CF交于点
,直线AG与直线CF交于点 求证
求证 .小明同学的思路是这样的:通过证明
.小明同学的思路是这样的:通过证明 ∽
∽ 得到
得到 ,从而得到
,从而得到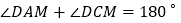 ,继续推理就可以使问题得到解决.
,继续推理就可以使问题得到解决. 请根据小明的思路,求证:
请根据小明的思路,求证: ;
; 爱动脑筋的小明把问题做了进一步思考,他想:如果把题目的“等边
爱动脑筋的小明把问题做了进一步思考,他想:如果把题目的“等边 ”改成“等腰直角
”改成“等腰直角 ,其中
,其中 ,
, ”,如图二,
”,如图二, 中的结论还成立吗?如果成立,求此时线段BM的最大值.
中的结论还成立吗?如果成立,求此时线段BM的最大值. 小明继续大胆设问:如图三,在
小明继续大胆设问:如图三,在 中,
中, ,
, ,将这样的
,将这样的 按照题目中的方式旋转
按照题目中的方式旋转 ,请直接写出AG与CF的位置关系以及线段BM的变化范围.
,请直接写出AG与CF的位置关系以及线段BM的变化范围.
相关试题

