【题目】已知王亮家、公园、新华书店在一条直线上,下面的图象反映的过程是:王亮从家跑步去公园,在那里锻炼了一阵后又走到新华书店去买书,然后散步走回家.其中![]() 表示时间,
表示时间,![]() 表示王亮离家的距离.
表示王亮离家的距离.

根据图象回答:
(1)公园离王亮家 ![]() ,王亮从家到公园用了
,王亮从家到公园用了 ![]() ;
;
(2)公园离新华书店 ![]() ;
;
(3)王亮在新华书店逗留了 ![]() ;
;
(4)王亮从新华书店回家的平均速度是多少?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根据观察函数图象的纵坐标,可得距离,观察函数图象的横坐标,可得时间;
(2)根据观察函数图象的纵坐标,利用纵坐标的差可求出公园与新华书店的距离;
(3)观察函数图象的横坐标,利用65-45可得在新华书店停留的时间;
(4)根据函数图象中的数据利用路程÷时间即可以求得王亮从书店回家的平均速度.
(1)由函数图象可得,公园离王亮家2.5千米,王亮从家到公园用了20![]() ;
;
故答案为:2.5;20;
(2)公园与新华书店的距离=2.5-1.5=1![]() ;
;
故答案为:1;
(3)由函数图象可得,
王亮在书店停留了:65-45=20(分钟),
故答案为:20;
(4)![]()
所以,王亮从书店回家的平均速度是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件之一能使平行四边形ABCD是菱形的为_____________.
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区准备新建
 个停车位,以解决小区停车难的问题。已知新建
个停车位,以解决小区停车难的问题。已知新建 个地上停车位和
个地上停车位和 个地下停车位共需
个地下停车位共需 万元:新建
万元:新建 个地上停车位和
个地上停车位和 个地下停车位共需
个地下停车位共需 万元,
万元,(1)该小区新建
 个地上停车位和
个地上停车位和 个地下停车位各需多少万元?
个地下停车位各需多少万元?(2)若该小区新建车位的投资金额超过
 万元而不超过
万元而不超过 万元,问共有几种建造方案?
万元,问共有几种建造方案?(3)对(2)中的几种建造方案中,哪种方案的投资最少?并求出最少投资金额.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,点P是(不与点A,B重合)为半圆上一点.将图形沿BP折叠,分别得到点A’,O’.设∠ABP=α.

(1)当α=10°时,∠ABA’= ____度;
(2)当点O’落在弧
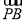 上时,求出α的度数.
上时,求出α的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形.
(2)若AB=5,BD=8,求矩形AODE的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从背面相同的同一副扑克牌中取出红桃9张、黑桃10张、方块11张,现将这些牌洗匀背面朝上放在桌面上.
(1)求从中抽出一张牌是红桃的概率;
(2)现从桌面上先抽掉若干张黑桃,再放入与抽掉的黑桃张数相同的红桃,并洗匀且背面都朝上排开后,随机抽一张是红桃的概率不小于
 ,问至少抽掉了多少张黑桃?
,问至少抽掉了多少张黑桃?(3)若先从桌面上抽掉9张红桃和m(m>6)张黑桃后,再在桌面抽出一张牌.
①当m为何值时,事件“再抽出的这张牌是方块”为必然事件?
②当m为何值时,事件“再抽出的这张牌是方块”为随机事件?并求出这个事件的概率的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OP1A1B1,A1P2A2B2,A2P3A3B3,……,An-1PnAnBn都是正方形,对角线OA1,A1A2,A2A3,……,An-1An都在y轴上(n≥1的整数),点P1(x1,y1),P2(x2,y2),……,Pn(xn,yn)在反比例函数y=
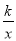 (x>0)的图象上,并已知B1(-1,1).
(x>0)的图象上,并已知B1(-1,1).
(1)求反比例函数y=
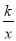 的解析式;
的解析式;(2)求点P2和P3的坐标;
(3)由(1)、(2)的结果或规律试猜想并直接写出:△PnBnO的面积为 ,点Pn的坐标为______(用含n的式子表示).
相关试题

