【题目】如图,在△ABC中,动点P在∠ABC的平分线BD上,动点M在BC边上,若BC=3,∠ABC=45°,则PM+PC的最小值是( )

A. 2 B. ![]() C.
C. ![]() D. 3
D. 3
参考答案:
【答案】B
【解析】分析:截取BE=BM,所以△BEP≌△BMP(SAS),根据点到直线的距离垂线段最短可知CE⊥AB,根据解直角三角形即可求解.
详解:如图:
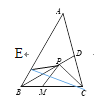
在AB上截取BE=BN,在△BEP和△BMP中,
 ,
,
∴△BEP≌△BMP(SAS),
∴MP=EP.
连接CE,
即:CE![]() PE+PC
PE+PC
当CE![]() PE+PC
PE+PC
即:CE与BP的交点即为点P,
当CE⊥AB时,CE最短(点到直线的距离垂线段最短).
∵∠ABC=45°,
∴∠EBC=∠BCE=45°.
∴sin∠EBC=![]() ,且BC=3,
,且BC=3,
∴EC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:点P是
 内一点.
内一点.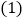 求证:
求证: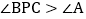 ;
; 若PB平分
若PB平分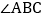 ,PC平分
,PC平分 ,
,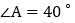 ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;
(1)如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数;
(2)如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由.
(3)如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=k1x+2与反比例函数
 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
(1)k1= , k2=;
(2)根据函数图象可知,当y1>y2时,x的取值范围是;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 为
为 的角平分线上的一点,点
的角平分线上的一点,点 在边
在边 上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边
上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边 上取一点
上取一点 ,使得
,使得 ,这时他发现
,这时他发现 与
与 之间有一定的数量关系,请你写出
之间有一定的数量关系,请你写出 与
与 的数量关系__________.
的数量关系__________.
相关试题

