【题目】已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
A. 当a=1时,函数图象过点(-1,1)
B. 当a=-2时,函数图象与x轴没有交点
C. 若a>0,则当x≥1时,y随x的增大而减小
D. 若a<0,则当x≤1时,y随x的增大而增大
参考答案:
【答案】D
【解析】
把a=1,x=-1代入y=ax![]() -2ax-1,于是得到函数图象不经过点(-1,1),根据△=8>0,得到函数图象与x轴有两个交点,根据抛物线的对称轴为直线x=
-2ax-1,于是得到函数图象不经过点(-1,1),根据△=8>0,得到函数图象与x轴有两个交点,根据抛物线的对称轴为直线x=![]() =1断二次函数的增减性
=1断二次函数的增减性
A.∵当a=1,=-1时,y=1+2-1=2,
∴函数图象不经过点(-1,1),故错误;
B.∵当a=-2时,△=4![]() -4
-4![]() (-2)×(-1)=8>0,
(-2)×(-1)=8>0,
∴函数图象与轴有两个交点,故错误
C.∵抛物线的对称轴为直线x![]() =1,
=1,
∴若a>0,则当x≥1时,y随x的增大而増大,故错
误
D.∵抛物线的对称轴为直线x![]() =1,
=1,
∴若a<0,则当x≤1时,y随x的增大而增大,故正确
故选D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(a,0),B(0,b),且a、b满足
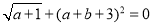 , ABCD的边AD与y轴交于点E,且E为AD中点,双曲线
, ABCD的边AD与y轴交于点E,且E为AD中点,双曲线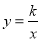 经过C、D两点.
经过C、D两点.(1)求k的值;
(2)点P在双曲线
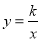 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;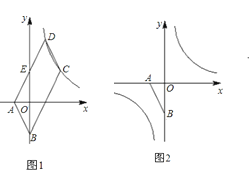
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班准备外出春游,有3名教师参加。有甲乙两家旅行社,其收费标准都一样,但都表示可以优惠师生.甲旅行社承诺:教师免费,学生按8折收费;乙旅行社承诺:师生一律按7折收费.
问:(1)如果由旅行社筹办春游活动,在什么条件下,两家旅行社所收费用相等.
(2)如果这个班有45名学生,选择哪家旅行社较恰当.请说明选择的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>x+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:
(1)探究:
①数轴上表示5和2的两点之间的距离是___.
②数轴上表示2和6的两点之间的距离是___.
③数轴上表示4和3的两点之间的距离是___.
(2)归纳:
一般的,数轴上表示数m和数n的两点之间的距离等于|mn|.
(3)应用:
①如果表示数a和3的两点之间的距离是7,则可记为:|a3|=7,那么a=___.
②若数轴上表示数a的点位于4与3之间,求|a+4|+|a3|的值.
-
科目: 来源: 题型:
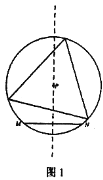
查看答案和解析>>【题目】定义:如图l所示,给定线段MN及其垂直平分线上一点P。若以点P为圆心,PM为半径的优弧(或半圆弧)MN上存在三个点可以作为一个等边三角形的顶点,则称点P为线段MN的“三足点”,特别的,若这样的等边三角形只存在一个,则称点P为线段MN的“强三足点”。
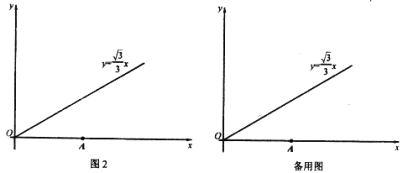
问题:如图2所示,平面直角坐标系xOy中,点A的坐标为(2
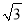 ,0),点B在射线y=
,0),点B在射线y=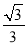 x(x≥0)上。
x(x≥0)上。(1)在点C(
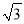 ,0),D(
,0),D(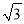 ,1),E(
,1),E(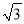 ,-2)中,可以成为线段OA的“三足点”的是__________.
,-2)中,可以成为线段OA的“三足点”的是__________.(2)若第一象限内存在一点Q既是线段OA的“三足点”,又是线段OB的“强三足点”,求点B的坐标。
(3)在(2)的条件下,以点A为圆心,AB为半径作圆,假设该圆与x轴交点中右侧一个为H,圆上一动点K从H出发,绕A顺时针旋转180°后停止,设点K出发后转过的角度为
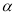 (0°<
(0°< 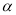 ≤180°),若线段OB与AK不存在公共“三足点”,请直接写出
≤180°),若线段OB与AK不存在公共“三足点”,请直接写出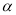 的取值范围是_______________。
的取值范围是_______________。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC与Rt△ABD中,
 ,
, ,AC、BD相交于点G,过点A作
,AC、BD相交于点G,过点A作 交CB的延长线于点E,过点B作
交CB的延长线于点E,过点B作 交DA的延长线于点F,AE、BF相交于点H.
交DA的延长线于点F,AE、BF相交于点H.
(1)证明:ΔABD≌△BAC.
(2)证明:四边形AHBG是菱形.
(3)若AB=BC,证明四边形AHBG是正方形.
相关试题

