【题目】数轴上A,B,C三点对应的数a,b,c满足(a+40)2+|b+10|=0,B为线段AC的中点.

(1)直接写出A,B,C对应的数a,b,c的值.
(2)如图1,点D表示的数为10,点P,Q分别从A,D同时出发匀速相向运动,点P的速度为6个单位/秒,点Q的速度为1个单位/秒.当点P运动到C后迅速以原速返回到A又折返向C点运动;点Q运动至B点后停止运动,同时P点也停止运动.求在此运动过程中P,Q两点相遇点在数轴上对应的数.
(3)如图2,M,N为A,C之间两点(点M在N左边,且它们不与A,C重合),E,F分别为AN,CM的中点,求![]() 的值.
的值.
参考答案:
【答案】(1)a=﹣40,b=﹣10,c=20;(2)P,Q两点相遇点在数轴上对应的数为﹣4或![]() ;(3)
;(3)![]() =2.
=2.
【解析】
(1)根据(a+40)2+|b+10|=0,可求出a、b的值,B为线段AC的中点.进而可求出c的值;
(2)分两种情况进行解答,一种是在A、D之间首次相遇,二是点P到C后返回追及Q相遇,设运动时间,根据相遇、追及问题数量关系列方程求出时间,进而求出相应时所对应的数;
(3)根据线段的中点的意义,用中点线段EF表示AC后即可得出答案.
解:(1)∵(a+40)2+|b+10|=0,
∴a=﹣40,b=﹣10,
∵B为线段AC的中点,
∴![]() =﹣10,
=﹣10,
∴c=20,
即:a=﹣40,b=﹣10,c=20;
(2)如图1,设运动的时间为t秒,
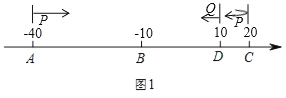
①当P与Q第一次相遇时,有6t+t=10﹣(﹣40),
解得,t=![]() ,
,
此时相遇点对应的数为10﹣![]() =
=![]() ;
;
②当点P到C返回追上点Q时,有6t﹣60=t+10,
解得,t=14,
此时相遇点对应的数为10﹣14=﹣4,
答:在此运动过程中P,Q两点相遇点在数轴上对应的数为﹣4或![]() ;
;
(3)如图2,∵E,F分别为AN,CM的中点,
∴AN=2EN,CM=2MF,
∴AC=2EN+2MF﹣MN
∴![]() =
=![]() =
=![]() =
=![]() =2,
=2,
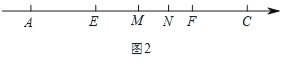
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式:
①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn,你认为其中正确的有( )

A. ①② B. ③④ C. ①②③ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 是线段
是线段 上任一点,
上任一点, ,
, 两点分别从
两点分别从 同时向
同时向 点运动,且
点运动,且 点的运动速度为
点的运动速度为 ,
, 点的运动速度为
点的运动速度为 ,运动的时间为
,运动的时间为 .
.(1)若
 ,
,①运动
 后,求
后,求 的长;
的长;②当
 在线段
在线段 上运动时,试说明
上运动时,试说明 ;
;(2)如果
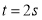 时,
时, ,试探索
,试探索 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=
 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>

 的x的取值范围;
的x的取值范围;(3)若点P在x轴上,且S△ACP=
 S△BOC,求点P的坐标.
S△BOC,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校以随机抽样的方式开展了“中学生喜欢数学的程度”的问卷调查,调查的结果分为A(不喜欢)、B(一般)、C(比较喜欢)、D(非常喜欢)四个等级,图1、图2是根据采集的数据绘制的两幅不完整的统计图.
请根据统计图提供的信息,回答下列问题:
(1)C等级所占的圆心角为________°;
(2)请直接在图2中补全条形统计图;
(3)若该校有学生1000人,请根据调查结果,估计“比较喜欢”的学生人数为多少人.
某校“中学生喜欢数学的程度”的扇形统计图 某校“中学生喜欢数学的程度”的条形统计图

-
科目: 来源: 题型:
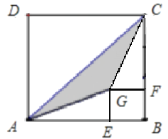
查看答案和解析>>【题目】如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
相关试题

