【题目】某运输公司承担了某标段的土方运输任务,公司已派出大小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车每次共35吨,3辆大型渣土运输车和2辆小型渣土运输车每次共运40吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?
(2)该运输公司决定派出大小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不小于150吨,问该运输公司最多派出几辆小型渣土运输车?
参考答案:
【答案】(1)一辆大型渣土运输车一次运输10吨,一辆小型渣土运输车一次运输5吨;(2)该运输公司最多派出10辆小型渣土运输车.
【解析】整体分析:
(1)设一辆大型渣土运输车一次运输x吨,一辆小型渣土运输车一次运输y吨,根据题中的相等关系列二元一次方程组;(2)根据大小两种型号的渣土运输车共20辆每次运输土方总量不小于150吨,列不等式,由a的取值范围确定a的值.
解:(1)设一辆大型渣土运输车一次运输x吨,一辆小型渣土运输车一次运输y吨,
![]() ,
,
解得![]() .
.
即一辆大型渣土运输车一次运输10吨,一辆小型渣土运输车一次运输5吨;
(2)设该运输公司派出a辆小型渣土运输车,
由题意可得,10(20﹣a)+5a≥150,
解得a≤10.
∵a是整数,
∴a最大为10,
∴该运输公司最多派出10辆小型渣土运输车.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
1
°
x
7
﹣3
…
(1)可知x= ,= ,°= ;
(2)试判断第2016个格子中的数是多少?并给出相应的理由.
(3)判断:前n个格子中所填整数之和是否可能为2016?若能,求出n的值,若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
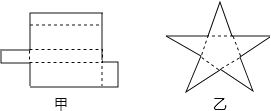
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情填,
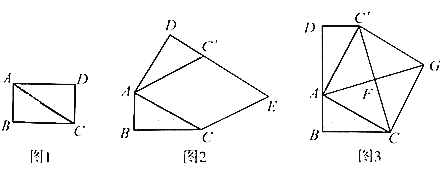
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动,如图1,将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD、并且量得AB=2cm,AC=4cm.
操作发现:
(1)将图1中的△ACD以点A为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到加图2所示的△AC′D,过点C作AC′的平行线,与DC′的延长线交于点E,则四边形ACEC'的形状是_________;
(2)创新小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B,A,D三点在同一条直线上,得到如图3所示的△AC′D,连接CC′,取CC'的中点F,连精AF并延长到点G,使FG=AF,连接CG,C′G,得到四边形ACGC′,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至A′点,A′C与BC′相交于点H.如图4所示,连接CC',试求CH的长度.
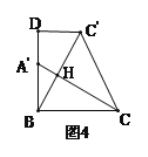
-
科目: 来源: 题型:
查看答案和解析>>【题目】701班小强买了张100元的深圳通乘车卡,如果他乘车的次数用
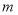 表示,则记录他每次乘车后的余额n (元)如下表:
表示,则记录他每次乘车后的余额n (元)如下表: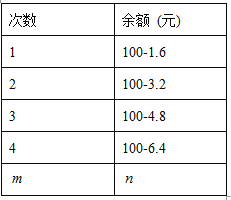
(1)写出余额n与乘车的次数m的关系式.
(2)利用上述关系式计算小强乘了23次车还剩下多少元?
(3)小强最多能乘几次车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B分别为数轴上的两点,点A表示的数是﹣30,点B表示的数是50.

(1)请写出A、B两点间的距离是 .
(2)现有一只蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左移动,同时另一只蚂蚁Q恰好从点A出发,以每秒2个单位长度的速度沿数轴向右移动,设两只蚂蚁在数轴上的点C相遇.求两只蚂蚁在数轴上的点C相遇时所用的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题
(1)“绿水青山就是金山银山”,某省2018年新建湿地公园和森林公园共42个,其中森林公园比湿地公园多4个.问该省2018年新建湿地公园和森林公园各多少个?
(2)某市大市场进行高端的家用电器销售,每件电器的进价是2000元,若按标价的八折销售该电器一件,则利润率为20%.求:
①该电器的标价是多少元?
②现如果按同一标价的九折销售该电器一件,那么获得的利润为多少元?
相关试题

