Question

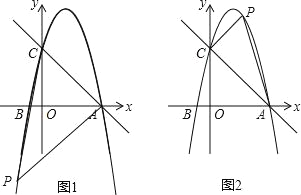
【题目】如图，在平面直角坐标系中，已知点A的坐标是（4，0），且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．

（1）求抛物线的表达式；

（2）在抛物线上是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由．

Answer 1

【答案】（1）抛物线的表达式是y=-x2+3x+4；（2）存在，点P的坐标为（-2，-6）或（2，6）．

【解析】

试题分析：（1）先由已知条件求出B、C两点的坐标，再设抛物线的表达式是y=ax2+bx+c，将A，B，C三点的坐标代入，利用待定系数法即可求出抛物线的表达式；

（2）由（1）中所求解析式可设点P的坐标为（m，-m2+3m+4）．当△ACP是以AC为直角边的直角三角形时，可分两种情况进行讨论：①以点A为直角顶点；②以点C为直角顶点；利用勾股定理分别列出关于m的方程，解方程即可．

试题解析：（1）∵点A的坐标是（4，0），

∴OA=4，

∵OA=OC=4OB，

∴OC=OA=4，OB=OA=1，

∴点C的坐标是（0，4），点B的坐标是（-1，0）．

设抛物线的表达式是y=ax2+bx+c，由题意得

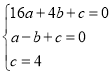，解得，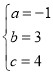

∴抛物线的表达式是y=-x2+3x+4；

（2）存在．

设点P的坐标为（m，-m2+3m+4）．

∵A（4，0），C（0，4），

∴AC2=42+42=32，AP2=（m-4）2+（-m2+3m+4）2，CP2=m2+（-m2+3m）2．

当△ACP是以AC为直角边的直角三角形时，可分两种情况：

①如图1，如果点A为直角顶点，那么AC2+AP2=CP2，

即32+（m-4）2+（-m2+3m+4）2=m2+（-m2+3m）2，

整理得m2-2m-8=0，

解得m1=-2，m2=4（不合题意舍去），

则点P的坐标为（-2，-6）；

②如图2，如果点C为直角顶点，那么AC2+CP2=AP2，

即32+m2+（-m2+3m）2=+（m-4）2+（-m2+3m+4）2，

整理得m2-2m=0，

解得m1=2，m2=0（不合题意舍去），

则点P的坐标为（2，6）；

综上所述，所有符合条件的点P的坐标为（-2，-6）或（2，6）．