【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图①,我们把一个四边形![]() 的四边中点
的四边中点![]() 依次连接起来得到的四边形
依次连接起来得到的四边形![]() 是平行四边形吗?
是平行四边形吗?
小敏在思考问题,有如下思路:连接![]() .
.


结合小敏的思路作答.
(1)若只改变图①中四边形![]() 的形状(如图②),则四边形
的形状(如图②),则四边形![]() 还是平行四边形吗?说明理由;
还是平行四边形吗?说明理由;
(参考小敏思考问题方法)
(2)如图②,在(1)的条件下,若连接![]() .
.
①当![]() 与
与![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是矩形,写出结论并证明;
是矩形,写出结论并证明;
②当![]() 与
与![]() 满足____时,四边形
满足____时,四边形![]() 是正方形.
是正方形.
参考答案:
【答案】(1)是,理由见解析;(2)①AC⊥BD,证明见解析;②AC⊥BD且AC=BD
【解析】
(1)连接AC,根据三角形中位线的性质得到EF∥AC,EF=![]() AC,然后根据平行四边形判定定理即可得到结论;
AC,然后根据平行四边形判定定理即可得到结论;
(2)①根据平行线的性质得到GH⊥BD,GH⊥GF,于是得到∠HGF=90°,根据矩形的判定定理即可得到结论;
②在①基础上,只要证明∠EHG=90°即可;
解:(1)四边形EFGH是平行四边形,理由如下:
如图2,连接AC,
∵E是AB的中点,F是BC的中点,
∴EF∥AC,EF=![]() AC,
AC,
同理HG∥AC,HG=![]() AC,
AC,
综上可得:EF∥HG,EF=HG,
故四边形EFGH是平行四边形;

(2)①当AC⊥BD时,四边形EFGH为矩形;
理由如下:
同(1)得:四边形EFGH是平行四边形,
∵AC⊥BD,GH∥AC,
∴GH⊥BD,
∵GF∥BD,
∴GH⊥GF,
∴∠HGF=90°,
∴四边形EFGH为矩形;

②结论:当AC⊥BD且AC=BD时,四边形EFGH是正方形.
理由:由①可知,AC=BD,四边形EFGH是菱形,
∵AC⊥BD,AC∥HG,
∴HG⊥BD,
∵EH∥BD,
∴EH⊥HG,
∴∠EHG=90°,
∴四边形EFGH是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(4,3)是反比例函数y=
 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y= 的图象于点P.
的图象于点P.(1)求反比例函数y=
 的表达式;
的表达式;(2)求点B的坐标;
(3)求△OAP的面积.

-
科目: 来源: 题型:
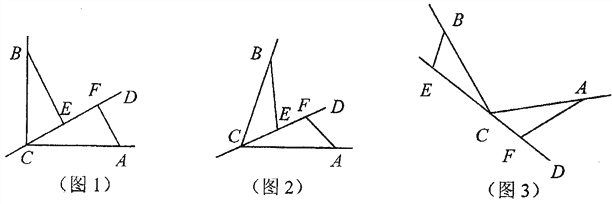
查看答案和解析>>【题目】已知CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠
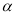 .
.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
①如图1若∠BCA=90°,∠
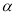 =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
=90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.②如图2,若0°<∠BCA<180°, 请添加一个关于∠
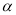 与∠BCA关系的条件___ ____使①中的结论仍然成立;
与∠BCA关系的条件___ ____使①中的结论仍然成立;(2)如图3,若直线CD经过∠BCA的外部,∠
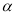 =∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
=∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2013的坐标为

A. (2,1006)B. (1008,0)C. ( -1006,0)D. (1,-1007)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一批单价为20元的商品,若每件按30元的价格销售时,每天能卖出60件;若每件按50元的价格销售时,每天能卖出20件,假定每天销售件数y(件)与销售价格x(元/件)满足y=kx+b.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不考虑其他因素的情况下,每件商品销售价格定为多少元时才能使每天获得的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:(1)
 (用代入消元法);(2)
(用代入消元法);(2) (用加减消元法)
(用加减消元法) -
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米
 小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点,过了5秒后,测得小汽车所在的B点与车速检测仪A之间的距离为100米.
小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点,过了5秒后,测得小汽车所在的B点与车速检测仪A之间的距离为100米. 求BC间的距离;
求BC间的距离; 这辆小汽车超速了吗?请说明理由.
这辆小汽车超速了吗?请说明理由.
【答案】这辆小汽车没有超速.
【解析】
(1)根据勾股定理求出BC的长;
(2)直接求出小汽车的时速,进行比较得出答案.(1)在Rt△ABC中,AC=60 m,
AB=100 m,且AB为斜边,根据勾股定理,得BC=80 m.
(2)这辆小汽车没有超速.
理由:∵80÷5=16(m/s),
而16 m/s=57.6 km/h,57.6<70,
∴这辆小汽车没有超速.
【点睛】
考查勾股定理的应用,熟练掌握勾股定理是解题的关键.
【题型】解答题
【结束】
19【题目】已知:如图,线段AC和BD相交于点G,连接AB,CD,E是CD上一点,F是DG上一点,
 ,且
,且 .
. 求证:
求证: ;
; 若
若 ,
, ,求
,求 的度数.
的度数.
相关试题

