【题目】如图,AB=2,BC=5,AB⊥BC于B,l⊥BC于C,点P自点B开始沿射线BC移动,过点P作PQ⊥PA交直线l于点Q. 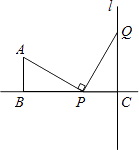
(1)求证:∠A=∠QPC;
(2)当点P运动到何处时,PA=PQ?并说明理由.
参考答案:
【答案】
(1)证明:∵PQ⊥AP,
∴∠ABP=90°
∴∠APB+∠QPC=90°,
∵AB⊥BC于点B,
∴∠A+∠APB=90°,
∴∠A=∠QPC;
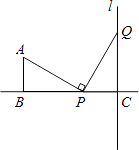
(2)解:当P运动到离C处距离为2时,PA=PQ,
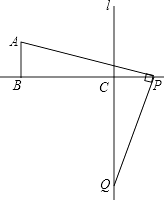
证明:当PC=2时,PC=AB,
在△ABP与△PCQ中,
∵ 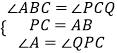 ,
,
∴△ABP≌△PCQ(ASA),
∴PA=PQ;
同理,BP=7时,PC=2也符合,
所以,点P运动到与点C距离为2时,PA=PQ
【解析】(1)根据直角三角形的两内角互余以及∠A+∠APB=90°,根据同角的余角相等,即可证得;(2)P运动到离C处距离为2时,PA=PQ,此时易证△ABP≌△PCQ,即可证得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片CD沿MN折叠(M,N在AD、BC上),AD∥BC,C′,D′为C、D的对称点,C′N交AD于E.
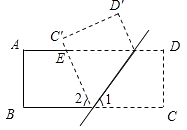
(1)若∠1=62°,则∠2=
(2)试判断△EMN的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在比例尺为1:20000的地图上,相距3cm的A,B两地的实际距离是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大鹏栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
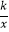 的一部分.请根据图中信息解析下列问题:
的一部分.请根据图中信息解析下列问题:
(1)求y与x的函数关系式;
(2)当x=16时,大棚内的温度约为多少度?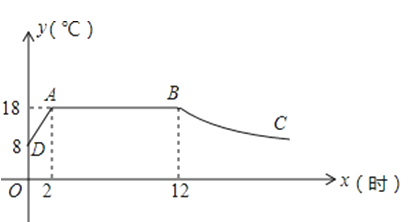
-
科目: 来源: 题型:
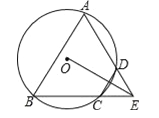
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.
(1)求证:∠A=∠AEB;
(2)如果DC⊥OE,求证:△ABE是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面图形上的任意两点P,Q,如果经过某种变换(如:平移、旋转、轴对称等)得到新图形上的对应点P′,Q′,保持P P′= Q Q′,我们把这种对应点连线相等的变换称为“同步变换”。对于三种变换: ①平移、②旋转、③轴对称,其中一定是“同步变换”的有(填序号)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程是一元二次方程的是( )
A.ax2+bx+c=0B.x2+2x=x2﹣1C.(x﹣1)(x﹣3)=0D.x=2
相关试题

