【题目】某学校在落实国家“营养餐”工程中,选用了A,B,C,D种不同类型的套餐.实行一段时间后,学校决定在全校范围内随机抽取部分学生对“你喜欢的套餐类型(必选且只选一种)”进行问卷调查,将调查情况整理后,绘制成如图所示的两个统计图.
请你根据以上信息解答下列问题:
(1)在这次调查中,一共抽取了名学生;
(2)请补全条形统计图;
(3)如果全校有1200名学生,请你估计其中喜欢D套餐的学生的人数.
参考答案:
【答案】
(1)100
(2)
解:100﹣40﹣20﹣10=30人.
补全条形统计图如图所示:

(3)
解:10÷100=10%,1200×10%=120人.
全校喜欢D套餐的学生的人数大约为120人
【解析】解:(1)40÷40%=100人,这次调查中一共抽取了100人.故答案为:100.
(1)根据喜爱A种套餐的人数和百分比求解即可;(2)依据总人数等于各部分的和可求得喜爱C套餐的人数;(3)先求得喜欢D套餐人数所占的百分比,然后用总人数乘百分比即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.

(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)
①求证:BG⊥GE;
②设DG与AB交于点M,若AG:AE=3:4,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顶点为M的抛物线y=a(x+1)2﹣4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
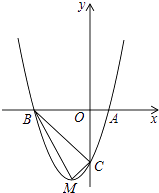
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算: +(1﹣
+(1﹣  )0﹣4cos45°.
)0﹣4cos45°.
(2)解方程组: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次测量活动中,小丽站在离树底部E处5m的B处仰望树顶C,仰角为30°,已知小丽的眼睛离地面的距离AB为1.65m,那么这棵树大约有多高?(结果精确到0.1m,参考数据:
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数y=
 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C. 
(1)求此反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.

(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:H为CE的中点;
(3)若BC=10,cosC= ,求AE的长.
,求AE的长.
相关试题

