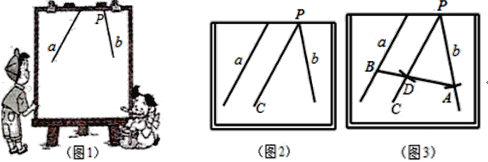
【题目】小明在做课本中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.
(1)请写出这种做法的理由.
(2)小明在此基础上又进行了如下操作和探究(如图3):
①以P为圆心,任意长为半径画圆弧,分别交直线b,PC于点A,D.
②连接AD并延长交直线a于点B,请直接写出图3中所有与∠PAB相等的角.
(3)请在图3画板内作出“直线a,b所成的跑到画板外面去的角”的平分线(画板内的部分),只要求作出图形,并保留作图痕迹.
参考答案:
【答案】(1)两直线平行,同位角相等;(2)∠PDA=∠BDC=∠1;(3)作图见解析.
【解析】
试题(1)根据平行线的性质得出即可;
(2)根据题意,有3个角与∠PAB相等.由等腰三角形的性质,可知∠PAB=∠PDA;又对顶角相等,可知∠BDC=∠PDA;由平行线性质,可知∠PDA=∠1.因此∠PAB=∠PDA=∠BDC=∠1;
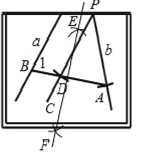
(3)作出线段AB的垂直平分线EF,由等腰三角形的性质可知,EF是顶角的平分线,故EF即为所求作的图形.
试题解析:(1)PC∥a(两直线平行,同位角相等);
(2)∠PAB=∠PDA=∠BDC=∠1,
如图,∵PA=PD,
∴∠PAB=∠PDA,
∵∠BDC=∠PDA(对顶角相等),
又∵PC∥a,
∴∠PDA=∠1,
∴∠PAB=∠PDA=∠BDC=∠1;
(3)如图,作线段AB的垂直平分线EF,则EF是所求作的图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把正整数1,2,3,4,…排列成如图所示的一个表.
(1)用一正方形在表中随意框住4个数,把其中最大的数记为x,另三个数用含x的式子表示出来,从大到小依次是 , , ;
(2)在(1)的前提下,当被框住的4个数之和等于984时,x位于该表的第几行第几列?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,∠A=120°.
(1)作线段AB的垂直平分线,分别交BC、AB于点M、N(要求用尺规作图,保留作图痕迹,不写作法);
(2)连接AM,判断△AMC的形状,并给予证明;
(3)求证:CM=2BM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】实验中学学生会倡议同学们将用不着的课外书籍捐赠给希望小学.学生会对全校的捐赠情况进行调查和分组统计后,将数据整理成如图所示统计图(图中信息不完整).已知A组和B组的人数比为1:5.
捐书人数分组统计表
组别
捐书数量x/本
人数
A
1≤x<10
a
B
10≤x<20
100
C
20≤x<30
D
30≤x<40
E
x≥40

请结合以上信息解答下列问题:
(1)a= ,本次参加捐书的总人数是 ;
(2)先求出C组的人数,再补全“捐书人数分组统计图1”;
(3)扇形统计图中,B组所对应的圆心角的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC,AB分别相切于C,D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于M点.

(1)求证:点M是CF的中点;
(2)若E是 的中点,BC=a,写出求AE长的思路.
的中点,BC=a,写出求AE长的思路. -
科目: 来源: 题型:
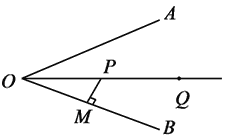
查看答案和解析>>【题目】已知:BOA是一条公路,河流OP恰好经过桥O平分∠AOB.
(1)如果要从P处移动到公路上路径最短,除图中所示PM外,还可以选择PN,求作这条路径,两条路径的关系是______,理由是___________.
(2)河流下游处有一点Q,如果要从P点出发,到达公路OA上的点C后再前往点Q,请你画出一条最短路径,表明点C的位置.
(3)D点在公路OB上,O点到D点的距离与C点相等,作出△CDP,求证:△CDP为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

相关试题

