搜索
【题目】如图，已知直线y1=﹣ 
x+1与x轴交于点A，与直线y2=﹣ 
x交于点B． 
（1）求△AOB的面积；
（2）求y1＞y2时x的取值范围．
参考答案：
【答案】
（1）解：由y1=﹣ 
x+1，
可知当y=0时，x=2，
∴点A的坐标是（2，0），
∴AO=2，
∵y1=﹣ x+1与x与直线y2=﹣ 
x交于点B，
∴B点的坐标是（﹣1，1.5），
∴△AOB的面积= ×2×1.5=1.5；
（2）解：由（1）可知交点B的坐标是（﹣1，1.5），
由函数图象可知y1＞y2时x＞﹣1．
【解析】（1）由函数的解析式可求出点A和点B的坐标，进而可求出△AOB的面积；（2）结合函数图象即可求出y1＞y2时x的取值范围．本题考查了一次函数与一元一次不等式、数形结合的数学思想，即学生利用图象解决问题的方法，这也是一元一次不等式与一次函数知识的具体应用．
-
科目： 来源： 题型：
查看答案和解析>>【题目】列方程解应用题
北京时间2015年7月31日，国际奥委会主席巴赫宣布：中国北京获得2022年第24界冬季奥林匹克运动会举办权，近期，新建北京至张家口铁路可行性研究报告已经获得国家发改委批复，铁路全长约180千米，按照设计，京张高铁列车的平均行驶速度是普通快车的1.5倍，用时比普通快车用时少了20分钟，求京张高铁列车的平均行驶速度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点B，E，C，F在一条直线上，AB=DF，AC=DE，∠A=∠D．
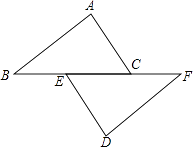
（1）求证：AC∥DE；
（2）若BF=13，EC=5，求BC的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】先化简：
÷ 
+ 
，再求当x+1与x+6互为相反数时代数式的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
小铭和小雨在学习过程中有如下一段对话：
小铭：“我知道一般当m≠n时，
≠
.可是我见到有这样一个神奇的等式：
=
（其中a，b为任意实数，且b≠0）．你相信它成立吗？”小雨：“我可以先给a，b取几组特殊值验证一下看看．”
完成下列任务：
（1）请选择两组你喜欢的、合适的a，b的值，分别代入阅读材料中的等式，写出代入后得到的具体等式并验证它们是否成立（在相应方框内打勾）；
① 当a= ，b= 时，等式 （□成立；□不成立）；
② 当a= ，b= 时，等式 （□成立；□不成立）．
（2）对于任意实数a，b（b≠0），通过计算说明
=是否成立． -
科目： 来源： 题型：
查看答案和解析>>【题目】在我们认识的多边形中，有很多轴对称图形．有些多边形，边数不同对称轴的条数也不同；有些多边形，边数相同但却有不同数目的对称轴．回答下列问题：
（1）非等边的等腰三角形有________条对称轴，非正方形的长方形有________条对称轴，等边三角形有___________条对称轴；
（2）观察下列一组凸多边形（实线画出），它们的共同点是只有1条对称轴，其中图1-2和图1-3都可以看作由图1-1修改得到的，仿照类似的修改方式，请你在图1-4和图1-5中，分别修改图1-2和图1-3，得到一个只有1条对称轴的凸五边形，并用实线画出所得的凸五边形；
（3）小明希望构造出一个恰好有2条对称轴的凸六边形，于是他选择修改长方形，图2中是他没有完成的图形，请用实线帮他补完整个图形；
（4）请你画一个恰好有3条对称轴的凸六边形，并用虚线标出对称轴．
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据频数分布表或频数分布直方图求加权平均数时，统计中常用各组的组中值代表各组的实际数据，把各组的频数看作相应组中值的权，请你依据以上知识，解决下面的实际问题．
为了解5路公共汽车的运营情况，公交部门统计了某天5路公共汽车每个运行班次的载客量，并按载客量的多少分成A，B，C，D四组，得到如下统计图：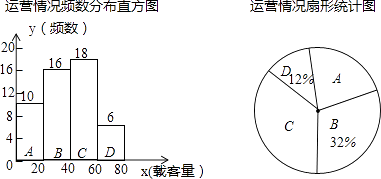
（1）求A组对应扇形圆心角的度数，并写出这天载客量的中位数所在的组；
（2）求这天5路公共汽车平均每班的载客量；
（3）如果一个月按30天计算，请估计5路公共汽车一个月的总载客量，并把结果用科学记数法表示出来．
相关试题
