【题目】(2016广西省贺州市第26题)如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.

参考答案:
【答案】(1)、y=![]() ;(2)、AD=5;(3)、(5,
;(2)、AD=5;(3)、(5,![]() )
)
【解析】
试题分析:(1)、利用矩形的性质和B点的坐标可求出A点的坐标,再利用待定系数法可求得抛物线的解析式;(2)、设AD=x,利用折叠的性质可知DE=AD,在Rt△BDE中,利用勾股定理可得到关于x的方程,可求得AD的长;(3)、由于O、A两点关于对称轴对称,所以连接OD,与对称轴的交点即为满足条件的点P,利用待定系数法可求得直线OD的解析式,再由抛物线解析式可求得对称轴方程,从而可求得P点坐标.
试题解析:(1)∵四边形ABCD是矩形,B(10,8),
∴A(10,0), 又抛物线经过A、E、O三点,把点的坐标代入抛物线解析式可得
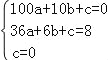 ,解得
,解得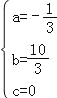 , ∴抛物线的解析式为y=﹣
, ∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x;
x;
(2)、由题意可知:AD=DE,BE=10﹣6=4,AB=8, 设AD=x,则ED=x,BD=AB﹣AD=8﹣x,
在Rt△BDE中,由勾股定理可知ED2=EB2+BD2,即x2=42+(8﹣x)2,解得x=5, ∴AD=5;
(3)、∵y=﹣![]() x2+
x2+![]() x, ∴其对称轴为x=5, ∵A、O两点关于对称轴对称, ∴PA=PO,
x, ∴其对称轴为x=5, ∵A、O两点关于对称轴对称, ∴PA=PO,
当P、O、D三点在一条直线上时,PA+PD=PO+PD=OD,此时△PAD的周长最小,
如图,连接OD交对称轴于点P,则该点即为满足条件的点P,
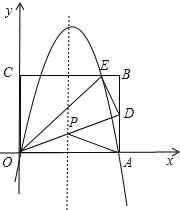
由(2)可知D点的坐标为(10,5),
设直线OD解析式为y=kx,把D点坐标代入可得5=10k,解得k=![]() , ∴直线OD解析式为y=
, ∴直线OD解析式为y=![]() x,
x,
令x=5,可得y=![]() , ∴P点坐标为(5,
, ∴P点坐标为(5,![]() ).
).
-
科目: 来源: 题型:
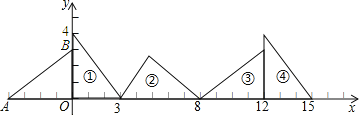
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(-4,0),B(0,3),对△OAB连续作旋转变换,依
次得到三角形(1)、三角形(2)、三角形(3)、三角形(4)、…,
(1)△AOB的面积是_____________;
(2)三角形(2016)的直角顶点的坐标是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a+a2=2a3
B.a2a3=a6
C.(a2)3=a5
D.a6÷a3=a3 -
科目: 来源: 题型:
查看答案和解析>>【题目】x1,x2是方程x2+2x﹣3=0的两个根,则代数式x12+3x1+x2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列数据85,88,73,88,79,85的众数是( )
A.88
B.73
C. 88,85
D.85 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题:
①一组对边平行且一组对角相等的四边形是平行四边形;
②对角线互相垂直且相等的四边形是正方形;
③顺次连接矩形四边中点得到的四边形是菱形;
④正五边形是轴对称图形,其中真命题有( )
A.①②③B.①③④C.①②④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广东省深圳市第23题)如图,抛物线
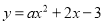 与
与 轴交于A、B两点,且B(1 , 0)。
轴交于A、B两点,且B(1 , 0)。(1)、求抛物线的解析式和点A的坐标;
(2)、如图1,点P是直线
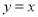 上的动点,当直线
上的动点,当直线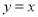 平分∠APB时,求点P的坐标;
平分∠APB时,求点P的坐标;(3)如图2,已知直线
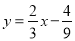 分别与
分别与 轴
轴 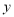 轴 交于C、F两点。点Q是直线CF下方的抛物线上的一个动点,过点Q作
轴 交于C、F两点。点Q是直线CF下方的抛物线上的一个动点,过点Q作 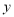 轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE。问以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由。
轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE。问以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由。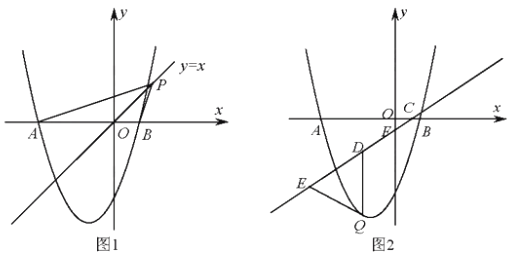
相关试题

