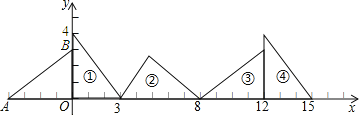
【题目】如图,在直角坐标系中,已知点A(-4,0),B(0,3),对△OAB连续作旋转变换,依
次得到三角形(1)、三角形(2)、三角形(3)、三角形(4)、…,
(1)△AOB的面积是_____________;
(2)三角形(2016)的直角顶点的坐标是_____________.
参考答案:
【答案】 6; (8064,0).
【解析】(1)根据点A、B的坐标求出OA、OB,再根据三角形的面积列式计算即可得解;
(2)观察不难发现,每3个三角形为一个循环组依次循环,用2013除以3,根据商是671可知三角形(2013)是第671个循环组的最后一个三角形,直角顶点在x轴上,再根据一个循环组的距离为12,进行计算即可得解.
解:(1)∵A(-4,0),B(0,3),
∴OA=4,OB=3,
∴△AOB的面积=![]() ×4×3=6;
×4×3=6;
(2)由图可知,每3个三角形为一个循环组依次循环,
∵2016=3×672,
∴三角形2016与三角形1的状态一样,
∴三角形2016的直角顶点的横坐标=672×12=8064,
∴三角形2016的顶点坐标为(8064, 0).
故答案为(8064,0).
“点睛”本题考查了坐标与图形变化-旋转,三角形的面积,仔细观察图形,发现每3个三角形为一个循环组依次循环是解题的关键,也是本题的难点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在∠AOB的两边上截取AO=BO,OC=OD,连接AD、BC交于点P,连接OP,则下列结论正确的是 ( )
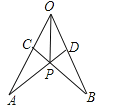
①△APC≌△BPD ②△ADO≌△BCO ③△AOP≌△BOP ④△OCP≌△ODP
A. ②③④ B. ①②③ C. ①②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个连续自然数的积为240,则这两个数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016湖南省岳阳市第24题)如图①,直线y=
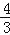 x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a+a2=2a3
B.a2a3=a6
C.(a2)3=a5
D.a6÷a3=a3 -
科目: 来源: 题型:
查看答案和解析>>【题目】x1,x2是方程x2+2x﹣3=0的两个根,则代数式x12+3x1+x2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广西省贺州市第26题)如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.

相关试题

