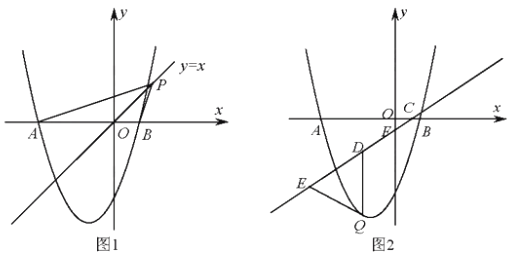
【题目】(2016广东省深圳市第23题)如图,抛物线![]() 与
与![]() 轴交于A、B两点,且B(1 , 0)。
轴交于A、B两点,且B(1 , 0)。
(1)、求抛物线的解析式和点A的坐标;
(2)、如图1,点P是直线![]() 上的动点,当直线
上的动点,当直线![]() 平分∠APB时,求点P的坐标;
平分∠APB时,求点P的坐标;
(3)如图2,已知直线![]() 分别与
分别与![]() 轴
轴 ![]() 轴 交于C、F两点。点Q是直线CF下方的抛物线上的一个动点,过点Q作
轴 交于C、F两点。点Q是直线CF下方的抛物线上的一个动点,过点Q作 ![]() 轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE。问以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由。
轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE。问以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由。
参考答案:
【答案】(1)、y=x![]() +2x-3 ,A(-3,0);(2)、(
+2x-3 ,A(-3,0);(2)、(![]() ,
,![]() );(3)、△QDE的面积最大值为
);(3)、△QDE的面积最大值为![]() .
.
【解析】
试题分析:(1)、把点B的坐标代入解析式得出函数解析式和点A的坐标;(2)、若y=x平分∠APB,则∠APO=∠BPO,若P点在x轴上方,PA与y轴交于![]() 点,从而得出△
点,从而得出△![]() ≌△OPB,从而得出点P的坐标;当点P在x轴下方时,不成立;(3)、作QH⊥CF,根据直线CF的解析式得出点C和点F的坐标,求出tan∠OFC的值,△QDE是以DQ为腰的等腰三角形,根据DQ=DE得出函数解析式,则当DQ=QE时则△DEQ的面积比DQ=DE时大,然后设点Q的坐标,求出函数解析式得出最大值.
≌△OPB,从而得出点P的坐标;当点P在x轴下方时,不成立;(3)、作QH⊥CF,根据直线CF的解析式得出点C和点F的坐标,求出tan∠OFC的值,△QDE是以DQ为腰的等腰三角形,根据DQ=DE得出函数解析式,则当DQ=QE时则△DEQ的面积比DQ=DE时大,然后设点Q的坐标,求出函数解析式得出最大值.
试题解析:(1)、把B(1,0)代入y=ax![]() +2x-3 得a+2-3=0,解得a=1
+2x-3 得a+2-3=0,解得a=1
∴y=x![]() +2x-3 ,A(-3,0)
+2x-3 ,A(-3,0)
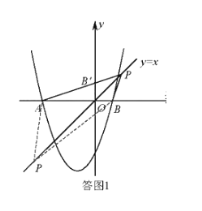
(2)、若y=x平分∠APB,则∠APO=∠BPO
如答图1,若P点在x轴上方,PA与y轴交于![]() 点 ∵∠POB=∠PO
点 ∵∠POB=∠PO![]() =45°,∠APO=∠BPO,PO=PO
=45°,∠APO=∠BPO,PO=PO
∴△![]() ≌△OPB ∴
≌△OPB ∴![]() =1,
=1,![]() ∴PA: y=3x+1 ∴
∴PA: y=3x+1 ∴![]()
若P点在x轴下方时,![]() 综上所述,点P的坐标为
综上所述,点P的坐标为![]()
(3)、如图2,作QH⊥CF, ![]() CF:y=
CF:y=![]() ,
,![]() C(
C(![]() ,0),F(0,
,0),F(0,![]() )
) ![]() tan∠OFC=
tan∠OFC=![]()
![]()
![]() DQ∥y轴
DQ∥y轴 ![]() ∠QDH=∠MFD=∠OFC
∠QDH=∠MFD=∠OFC ![]() tan∠HDQ=
tan∠HDQ=![]()
不妨记DQ=1,则DH=![]() ,HQ=
,HQ=![]()
![]() △QDE是以DQ为腰的等腰三角形
△QDE是以DQ为腰的等腰三角形
![]() 若DQ=DE,则
若DQ=DE,则![]()
若DQ=QE,则![]()
![]()
![]() <
<![]()
![]() 当DQ=QE时则△DEQ的面积比DQ=DE时大
当DQ=QE时则△DEQ的面积比DQ=DE时大
设Q![]()
![]() 当DQ=t=
当DQ=t=![]()
![]()
![]()
![]()
![]() 以QD为腰的等腰△QDE的面积最大值为
以QD为腰的等腰△QDE的面积最大值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广西省贺州市第26题)如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列数据85,88,73,88,79,85的众数是( )
A.88
B.73
C. 88,85
D.85 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题:
①一组对边平行且一组对角相等的四边形是平行四边形;
②对角线互相垂直且相等的四边形是正方形;
③顺次连接矩形四边中点得到的四边形是菱形;
④正五边形是轴对称图形,其中真命题有( )
A.①②③B.①③④C.①②④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④
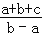 的最小值为3.
的最小值为3.其中,正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下面各组数据中,众数是3.5的是( )
A.4,3,4,3
B.1.5,2,2.5,3.5
C.3.5,4.5,3.5
D.6,4,3,2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在描述一组数据的集中趋势时,应用最广泛的是( )
A.众数
B.中位数
C.平均数
D.全体数据
相关试题

