【题目】菱形 ABCD 的对角线 AC=4,BD=2,以 AC 为边作正方形 ACEF,则 BF 的长为_____.
参考答案:
【答案】![]() 或
或![]()
【解析】
作出图形,根据菱形的对角线互相垂直平分求出AO、BO,然后分正方形在AC的两边两种情况补成以BF为斜边的Rt△BKF,然后求出BK、FK,再利用勾股定理列式计算即可得解.
解∵AC=4,BD=2,
∴AO=2,BO=1,
如图1,正方形ACEF在AC的左边时,过点B作BK⊥AF交FA于K,
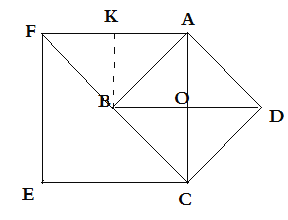
∴BK=AO=2,FK=AF-AK=3,
在Rt△BFK中,BF=![]() =
=![]() ,
,
如图,正方形ACEF在AC的右边时,过点B作BK⊥AF交FA的延长线于K
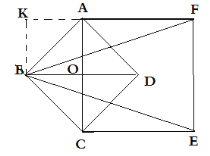
∴BK=AO=2,FK=AF+AK=5,
在Rt△BFK中,BF=![]() =
=![]() ,
,
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
(1)求证:DF与⊙O的位置关系并证明;
(2)求FG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形 ABCD 中,AD∥BC,DE⊥BC,垂足为点 E,连接 AC 交DE 于点 F,点 G 为 AF 的中点,∠ACD=2∠ACB,若 DC=5,则 AF 的长为___________.
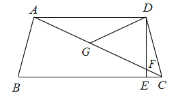
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长方形纸片 ABCD 折叠起来,使其对角顶点 A,C 重合,若其长 BC 为 9,宽 AB 为 3.
⑴求证:△AEF 是等腰三角形;
⑵EF= .
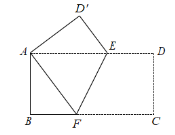
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y1=2x+2与直线 l2:y2=mx+8相交于点 P(2,b).
(1)求 b,m 的值;
(2)直接写出当 y1<y2 时,自变量 x 的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?
相关试题

