【题目】两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,图中AB=AC,AD=AE,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连结DC.
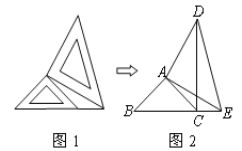
(1)图2中的全等三角形是_______________,并给予证明(说明:结论中不得含有未标识的字母);
(2)指出线段DC和线段BE的关系,并说明理由.
参考答案:
【答案】(1)△ACD≌△ABE,证明见解析;(2)线段DC和线段BE的关系是:垂直且相等,理由见解析.
【解析】
(1)根据SAS证明△ACD≌△ABE 即可;
(2)线段DC和线段BE的关系是:垂直且相等.利用全等三角形的性质即可证明.
解:(1)图2中的全等三角形是:△ACD≌△ABE.
证明:∵∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠EAD+∠CAE,
∴∠BAE=∠CAD,
在△ABE与△ACD中,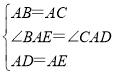 ,
,
∴△ACD≌△ABE(SAS).
故答案为:△ACD≌△ABE;
(2)线段DC和线段BE的关系是:垂直且相等.
理由:由(1)知:△ACD≌△ABE
∴DC=BE,∠ACD=∠B,
∵∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠ACD+∠ACB=90°,即∠BCD=90°,
∴BE⊥DC,
∴线段DC和线段BE的关系是:垂直且相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有五张正面分别标有数字﹣2,﹣1,0,1,2的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,0)的概率是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若OC是∠AOB内部的一条射线,则下列式子中,不能表示“OC是∠AOB的平分线”的是( )
A. ∠AOC=∠BOC B. ∠AOB=2∠BOC
C. ∠AOC=
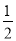 ∠AOB D. ∠AOC+∠BOC=∠AOB
∠AOB D. ∠AOC+∠BOC=∠AOB -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是△ABC的外角∠EAB的平分线AF上的一点,PD垂直平分BC,PG
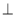 AB,求证:BG=AG+AC.
AB,求证:BG=AG+AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):

(1)根据记录的数据可知该厂星期四生产自行车________ 辆;
(2)根据记录的数据可知该厂本周实际生产自行车______辆;
(3)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖励15元;少生产一辆另扣20元,那么该厂工人这一周的工资总额是多少?
(4)若将上面第(3)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,在此方式下这一周工人的工资与按日计件的工资哪一个更多?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
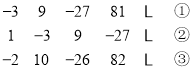
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系;
(3)设
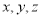 分别为第①②③行的2012个数,求
分别为第①②③行的2012个数,求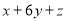 的值.
的值. -
科目: 来源: 题型:
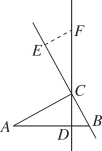
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)当点E运动多长时间时,CF=AB.请说明理由.
相关试题

