【题目】已知如图,圆锥的母线长6cm,底面半径是3cm,在B处有一只蚂蚁,在AC中点P处有一颗米粒,蚂蚁从B爬到P处的最短距离是( )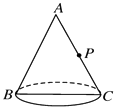
A.3 ![]() cm
cm
B.3 ![]() cm
cm
C.9cm
D.6cm
参考答案:
【答案】B
【解析】解:∵圆锥的侧面展开图是一个扇形,设该扇形的圆心角为n,
则: ![]() =
= ![]() ×2×3π,其中r=3,
×2×3π,其中r=3,
∴n=180°,如图所示:
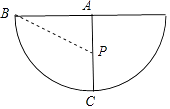
由题意可知,AB⊥AC,且点P为AC的中点,
在Rt△ABP中,AB=6,AP=3,
∴BP= ![]() =3
=3 ![]() cm,
cm,
故蚂蚁沿线段BP爬行,路程最短,最短的路程是3 ![]() cm.
cm.
【考点精析】本题主要考查了勾股定理的概念和弧长计算公式的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的才能正确解答此题.
-
科目: 来源: 题型:
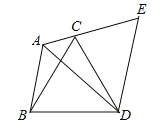
查看答案和解析>>【题目】已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求AD的长.
-
科目: 来源: 题型:
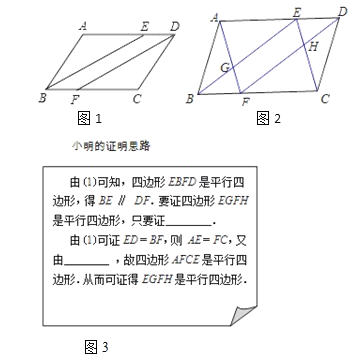
查看答案和解析>>【题目】如图1,ABCD中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.
(1)求证:四边形EBFD是平行四边形;
(2)如图2,小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图3)中补全他的证明思路,再在答题纸上写出规范的证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如
 .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:设
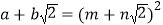 (其中
(其中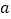 、
、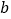 、
、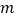 、
、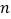 均为整数),则有
均为整数),则有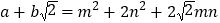 .
.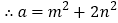 ,
,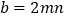 .这样小明就找到了一种把类似
.这样小明就找到了一种把类似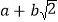 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)当
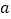 、
、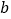 、
、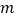 、
、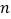 均为正整数时,若
均为正整数时,若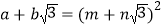 ,用含
,用含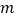 、
、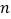 的式子分别表示
的式子分别表示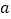 、
、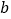 ,得:
,得: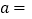 ,
,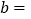 ;
;(2)利用所探索的结论,找一组正整数
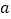 、
、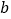 、
、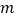 、
、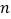 填空:
填空: 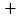
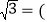
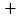
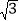
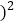 ;
;(3)若
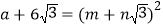 ,且
,且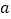 、
、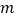 、
、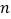 均为正整数,求
均为正整数,求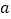 的值?
的值? -
科目: 来源: 题型:
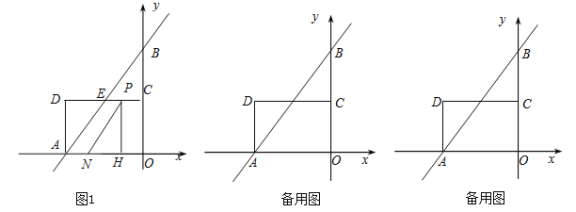
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线
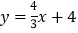 分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形(有一个角是直角的平行四边形).
分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形(有一个角是直角的平行四边形).(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作PHOA,垂足为H,连接NP.设点P的运动时间为t秒.
①若△NPH的面积为1,求t的值;
②点Q是点B关于点A的对称点,问BPPHHQ是否有最小值,如果有,直接写出相应的点P的坐标;如果没有,请说明理由.
-
科目: 来源: 题型:
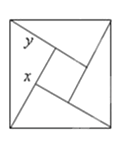
查看答案和解析>>【题目】如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的结论有______________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.

(1)请写出图中全等三角形(不再添加辅助线).
(2)求证:△ABE≌△CDF;
相关试题

