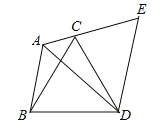
【题目】已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求AD的长.
参考答案:
【答案】8
【解析】
只要证明△ADE是等边三角形,即可推出∠EAD=60°,AD=AE,推出∠BAD=∠BAC-∠CAD=60°,推出AD=AE=AC+CE=AC+AB=3+5=8.
∵△ECD 由△ABD 绕点 D 顺时针旋转 60°而得:
∴AD=DE,∠BDA=∠CDE,
∴∠BDC=∠ADE=60°,∠ABD=∠ECD,
∵∠BAC=120°,∠BDC=60°,
∴∠BAC+∠BDC=180°,
∴∠ABD+∠ACD=180°,
∴∠ACD+∠ECD=180°,
∴A、C、E 共线,
∴△ADE 是等边三角形,
∴∠EAD=60°,AD=AE,
∴AD=AE=AC+CE=AC+AB=3+5=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为半径OH上一点,点E,F分别在矩形ABCD的边BC和CD上.
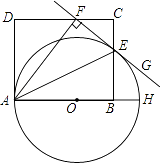
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点,且与y轴相交于点C,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点C的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为直角三角形,请直接写出所有符合条件的点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图案中,既是轴对称图形又是中心对称图形的个数为( )
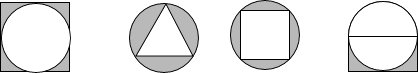
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
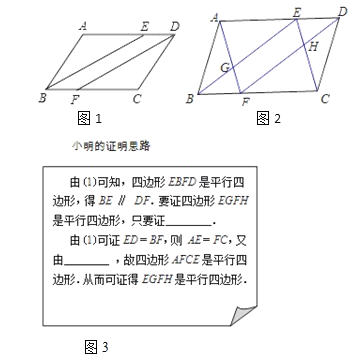
查看答案和解析>>【题目】如图1,ABCD中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.
(1)求证:四边形EBFD是平行四边形;
(2)如图2,小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图3)中补全他的证明思路,再在答题纸上写出规范的证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如
 .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:设
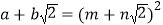 (其中
(其中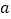 、
、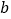 、
、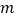 、
、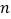 均为整数),则有
均为整数),则有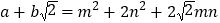 .
.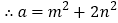 ,
,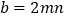 .这样小明就找到了一种把类似
.这样小明就找到了一种把类似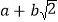 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)当
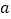 、
、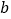 、
、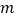 、
、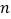 均为正整数时,若
均为正整数时,若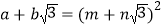 ,用含
,用含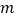 、
、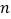 的式子分别表示
的式子分别表示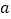 、
、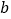 ,得:
,得: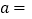 ,
,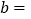 ;
;(2)利用所探索的结论,找一组正整数
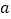 、
、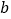 、
、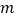 、
、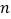 填空:
填空: 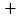
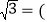
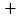
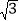
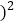 ;
;(3)若
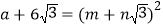 ,且
,且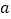 、
、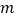 、
、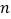 均为正整数,求
均为正整数,求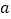 的值?
的值? -
科目: 来源: 题型:
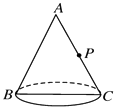
查看答案和解析>>【题目】已知如图,圆锥的母线长6cm,底面半径是3cm,在B处有一只蚂蚁,在AC中点P处有一颗米粒,蚂蚁从B爬到P处的最短距离是( )
A.3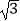 cm
cm
B.3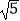 cm
cm
C.9cm
D.6cm
相关试题

