【题目】已知抛物线![]()
(1)若抛物线的顶点坐标为(2,-3),求b,c的值;
(2)若![]() ,是否存在实数x,使得相应的y的值为1,请说明理由;
,是否存在实数x,使得相应的y的值为1,请说明理由;
(3)若![]() 且抛物线在-2≤x≤2上的最小值是-3,求b的值.
且抛物线在-2≤x≤2上的最小值是-3,求b的值.
参考答案:
【答案】(1)b=2,c=1;
(2)存在两个不同实数![]() ,使得相应
,使得相应![]() ,理由见解析;(3)
,理由见解析;(3)![]() 或
或![]()
【解析】分析(1) 由顶点坐标为(2,-3)化为 顶点![]() 即可求解.(2)把y=1,c=-b,代入
即可求解.(2)把y=1,c=-b,代入![]() 化为
化为![]() ,根据求根公式即可求解.(3)把c=b+2代入化为
,根据求根公式即可求解.(3)把c=b+2代入化为![]() ,由对称轴为
,由对称轴为![]() ,分两种情况讨论即可.
,分两种情况讨论即可.
(本小题满分12分)
解:(1![]() ),b=2,c=1 (2)由
),b=2,c=1 (2)由![]() ,b+c=0 得
,b+c=0 得 ![]() ,
,![]() ,
,![]()
所以方程 ![]() 有两个不相等实数根,
有两个不相等实数根,
即存在两个不同实数![]() ,使得相应
,使得相应![]()
(3)由c=b+2,则抛物线可化为![]() ,其对称轴为x=b,
,其对称轴为x=b,
①当x=b<-2时,则有抛物线在![]() 时取最小值为-3,此时
时取最小值为-3,此时![]() ,解得
,解得![]() ,不合题意
,不合题意
②当x=b>2时,则有抛物线在![]() 时取最小值为-3,此时
时取最小值为-3,此时
![]() ,解得
,解得![]() ,合题意
,合题意
当![]() ,则
,则![]() ,化简得:
,化简得:![]() ,解得:
,解得:
![]() (不合题意,舍去),
(不合题意,舍去),![]() .
.
综上:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4×
 ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 . 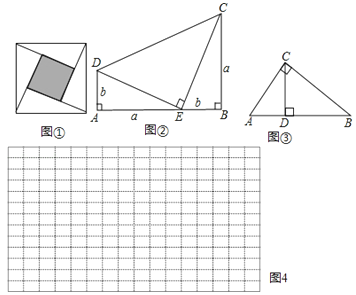
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,则斜边AB上的高CD的长为.
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2 , 画在如图4的网格中,并标出字母a、b所表示的线段. -
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC= b2+
b2+ ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB= c2+
c2+ a(b﹣a)
a(b﹣a)
∴ b2+
b2+ ab=
ab= c2+
c2+ a(b﹣a)
a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,_____________________叫作平行线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.
(1)求∠BDC的度数.
(2)求AC的长度.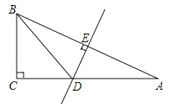
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.
, ,
, 
B.1, ,
, 
C.6a,7a,8a
D.2a,3a,4a -
科目: 来源: 题型:
查看答案和解析>>【题目】在式子-3<0,4x+3y>0,x=3,a2+2a+1≤8,x2+2xy+y2,x≠5,x2≥0中,不等式有( )
A. 2个 B. 3个 C. 4个 D. 5个
相关试题

