搜索
【题目】在△ABC中，已知∠A－∠B＝30°，∠C＝4∠B，求∠A，∠B，∠C的度数，并判断这个三角形的形状．
参考答案：
【答案】这个三角形是钝角三角形．
【解析】
首先根据三角形内角和定理和已知条件得到相等关系式6∠B＋30°＝180°,进而求得∠B的值;接下来根据条件即可求得∠A、∠C的度数, 从而得到三角形的类型.
解：因为∠A－∠B＝30°，所以∠A＝∠B＋30°.又因为∠C＝4∠B，
且∠A＋∠B＋∠C＝180°，即6∠B＋30°＝180°，所以∠B＝25°，
则∠A＝55°，∠C＝100°，所以这个三角形是钝角三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，AB=6，AD=8，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE于G，BG=4
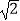，则四边形AECD的周长为（ ）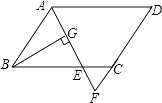 
A.20
B.21
C.22
D.23 -
科目： 来源： 题型：
查看答案和解析>>【题目】据统计，2019年第一季度，深圳新出台的小微企业普惠性减税政策合计减税13.53亿元．“13.53亿”用科学记数法表示为（ ）
A. 13.53×102B. 1.353×109C. 0.1353×102D. 1.353×102
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标中，△ABC的三个顶点的坐标分别是A(－2,3)，B(－4，－1)，C(2,0)，将△ABC沿x轴方向向左平移_______至△A1B1C1的位置，点A、B、C的对应点分别是A1、B1、C1，使点C1在原点处．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，对角线AC，BD相交于点E，∠CBD=90°，BC=4，BE=ED=3，AC=10，则四边形ABCD的面积为（ ）
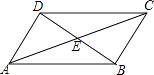
A.6
B.12
C.20
D.24 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE．若∠CAE=65°，∠E=70°，且AD⊥BC，垂足为F，求∠BAC的度数．
-
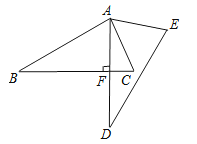
科目： 来源： 题型：
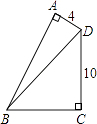
查看答案和解析>>【题目】如图，四边形ABCD中，∠A=∠C=90°，∠ABC=60°，AD=4，CD=10，则BD的长等于 ．
相关试题
