【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F. 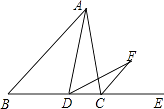
(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
参考答案:
【答案】
(1)证明:∵AC=BC,
∴∠B=∠BAC,
∵∠ACE=∠B+∠BAC,
∴∠BAC= ![]() ,
,
∵CF平分∠ACE,
∴∠ACF=∠ECF= ![]() ,
,
∴∠BAC=∠ACF,
∴CF∥AB
(2)解:∵∠BAC=∠ACF,∠B=∠BAC,∠ADF=∠B,
∴∠ACF=∠ADF,
∵∠ADF+∠CAD+∠AGD=180°,∠ACF+∠F+∠CGF=180°,
又∵∠AGD=∠CGF,
∴∠F=∠CAD=20°
【解析】(1)根据三角形的性质得到∠B=∠BAC,由三角形外角的性质得到∠ACE=∠B+∠BAC,求得∠BAC= ![]() ,由角平分线的定义得到∠ACF=∠ECF=
,由角平分线的定义得到∠ACF=∠ECF= ![]() ,等量代换得到∠BAC=∠ACF,根据平行线的判定定理即可得到结论;(2)由等量代换得到∠ACF=∠ADF,根据三角形的内角和得到∠ADF+∠CAD+∠AGD=180°,∠ACF+∠F+∠CGF=180°,由于∠AGD=∠CGF,即可得到结论.
,等量代换得到∠BAC=∠ACF,根据平行线的判定定理即可得到结论;(2)由等量代换得到∠ACF=∠ADF,根据三角形的内角和得到∠ADF+∠CAD+∠AGD=180°,∠ACF+∠F+∠CGF=180°,由于∠AGD=∠CGF,即可得到结论.
【考点精析】本题主要考查了平行线的判定和等腰三角形的性质的相关知识点,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式(3﹣b)x5+xa+x﹣6是关于x的二次三项式,求a2﹣b2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,点D为AC上一点,且BD=BC.将△BCD沿直线BD折叠后,点C落在AB上的点E处,若AE=DE,则∠A的度数为 .
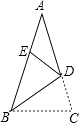
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:
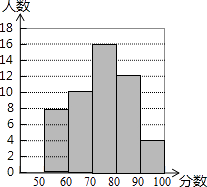
(1)本次选取参加测试的学生人数是;
(2)学生“信息素养”得分的中位数是;
(3)若把每组中各个分数用这组数据的中间值代替(如30﹣40分的中间值为35分),则参加测试的学生的平均分为分. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,
AB是圆片的直径.(注:结果保留π )
(1)把圆片沿数轴向右滚动半周,点B到达数轴上点C的位置,点C表示的数是数(填“无理”或“有理”),这个数是;
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3
①第次滚动后,A点距离原点最远;
②当圆片结束运动时,此时点A所表示的数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B对应的数分别为﹣1、3,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、点B的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为8?若存在,请求出x的值;若不存在,说明理由;
(3)现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,点P以6个单位长度/秒的速度同时从O点向左运动.当点A与点B之间的距离为3个单位长度时,求点P所对应的数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣2+8﹣1﹣5
(2)(﹣ )×3÷3×(﹣
)×3÷3×(﹣  )
)
(3)(﹣2)×3﹣(﹣8)÷(﹣2)2
(4)( ﹣1
﹣1  +
+ 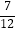 )÷(﹣
)÷(﹣ 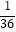 )
)
相关试题

