【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P,Q分别从A,B同时出发,当四边形APQC的面积最小时,经过的时间为( )

A. 1 s B. 2 s C. 3 s D. 4 s
参考答案:
【答案】C
【解析】
根据等量关系“四边形APQC的面积=三角形ABC的面积-三角形PBQ的面积”列出函数关系求最小值.
设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC-S△PBQ
=![]() ×12×6-
×12×6-![]() (6-t)×2t
(6-t)×2t
=t2-6t+36
=(t-3)2+27.
∴当t=3s时,S取得最小值.
故选:C.
-
科目: 来源: 题型:
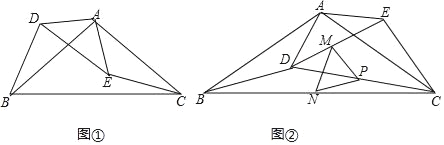
查看答案和解析>>【题目】如图①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求证:△ABD≌△ACE;
(2)把△ADE绕点A逆时针方向旋转到图②的位置,连接CD,点M、P、N分别为DE、DC、BC的中点,连接MN、PN、PM,判断△PMN的形状,并说明理由;
(3)在(2)中,把△ADE绕点A在平面内自由旋转,若AD=4,AB=6,请分别求出△PMN周长的最小值与最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=
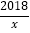 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为
 米,宽为
米,宽为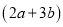 米的长方形草坪上修建两条宽为
米的长方形草坪上修建两条宽为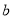 米的通道.
米的通道.
(1)剩余草坪的面积是多少平方米?
(2)当
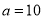 ,
,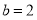 时,剩余草坪的面积是多少平方米?
时,剩余草坪的面积是多少平方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点
 是
是 的边
的边 上的一点,过点
上的一点,过点 作
作 ,
, ,
, ,
, 为垂足,再过点
为垂足,再过点 作
作 ,交
,交 于点
于点 ,且
,且 .
.
(1)求证:
 ;
;(2)求证:
 垂直平分
垂直平分 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,等边
 .
.(1)如图(1),若
 ,现有两点
,现有两点 、
、 分别从点
分别从点 、点
、点 同时出发,沿三角形的边顺时针运动,已知点
同时出发,沿三角形的边顺时针运动,已知点 的速度为
的速度为 ,点
,点 的速度为
的速度为 .当点
.当点 第一次到达
第一次到达 点时,
点时, 、
、 同时停止运动.点
同时停止运动.点 ,
, 运动______秒后,
运动______秒后, 为等腰三角形.
为等腰三角形.
(2)如图,点
 位于等边
位于等边 的内部,且
的内部,且 .将
.将 绕点
绕点 顺时针旋转
顺时针旋转 ,点
,点 的对应点为点
的对应点为点 .
.①依题意,补全图形;
②若
 ,
, ,求
,求 与
与 的面积比.
的面积比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
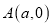 ,
,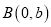 ,满足:
,满足: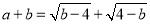 .
.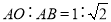 .
.(1)
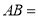 ______;
______;(2)点
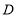 是
是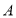 点左侧的
点左侧的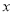 轴上一点,连接
轴上一点,连接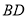 ,以
,以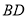 为直角边作等腰直角
为直角边作等腰直角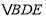 ,
,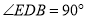 .连接
.连接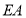 ,
,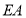 交
交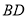 于点
于点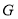 ;
;①求
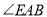 .
.②若
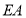 平分
平分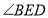 ,试求
,试求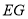 的长.
的长.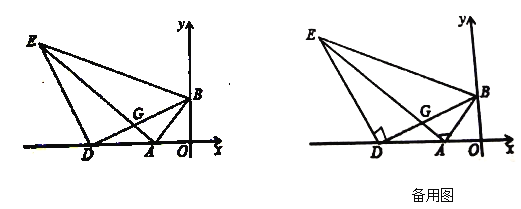
相关试题

