【题目】如图1,![]() ,
,![]() ,满足:
,满足:![]() .
.![]() .
.
(1)![]() ______;
______;
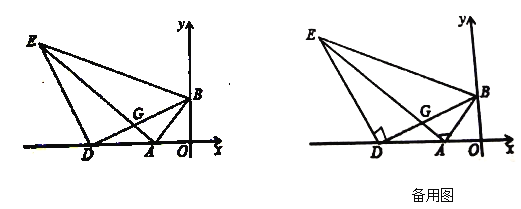
(2)点![]() 是
是![]() 点左侧的
点左侧的![]() 轴上一点,连接
轴上一点,连接![]() ,以
,以![]() 为直角边作等腰直角
为直角边作等腰直角![]() ,
,![]() .连接
.连接![]() ,
,![]() 交
交![]() 于点
于点![]() ;
;
①求![]() .
.
②若![]() 平分
平分![]() ,试求
,试求![]() 的长.
的长.
参考答案:
【答案】(1)![]() ;(2)①90°;②
;(2)①90°;②![]()
【解析】
(1)根据题意得出![]() ,求出b=4.得出a+b=0.a=-4,即可得出A、B的坐标,由勾股定理可得AB的长;
,求出b=4.得出a+b=0.a=-4,即可得出A、B的坐标,由勾股定理可得AB的长;
(2)①过点E作EH⊥x轴于点H,由AAS证明△EHD≌△DOB,得出DH=OB=OA=4,EH=OD.证出EH=AH.得出△EHA为等腰直角三角形.由等腰直角三角形的性质得出∠EAH=45°=∠BAO.得出∠EAB=90°即可;
②延长BA、ED相交于点H,由ASA证明△BEA≌△HEA,得出HA=BA=4![]() .得出BH=2AB=8
.得出BH=2AB=8![]() .证出∠DEG=∠DBH.由ASA证明△EDG≌△BDH,得出EG=BH=8
.证出∠DEG=∠DBH.由ASA证明△EDG≌△BDH,得出EG=BH=8![]() 即可.
即可.
(1)∵![]() ,
,
∴![]()
解得:b=4.
此时![]() ,
,
∴a+b=0.
∴a=-4,
∴A(-4,0)、B(0,4).
∴AB=![]() ;
;
(2)①如图1,过点E作EH⊥x轴于点H.则∠EDH+∠DEH=90°.

∵∠EDB=90°.
∴∠EDH+∠BDO=90°.
∴∠BDO=∠DEH.
在△EHD和△DOB中,
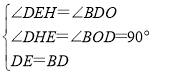
∴△EHD≌△DOB.
∴DH=OB=OA=4,EH=OD.
而AH=DH+AD=OA+AD=OD.
∴EH=AH.
∴△EHA为等腰直角三角形.
∴∠EAH=45°=∠BAO.
∴∠EAB=90°.
②如图2,延长BA、ED相交于点Q.

∵EA平分∠BEQ.
∴∠QEA=∠BEA.
由①得:∠EAB=90°=∠EAQ.
在△BEA和△QEA中,
 ,
,
∴△BEA≌△QEA.
∴QA=BA=![]() .
.
∴BQ=2AB=8![]() .
.
∵∠EDG=90°=∠GAB.且∠EGD=∠BGA.
∴∠DEG=∠DBQ.
在△EDG和△BDQ中,
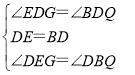
∴△EDG≌△BDH(ASA).
∴EG=BH=8![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P,Q分别从A,B同时出发,当四边形APQC的面积最小时,经过的时间为( )

A. 1 s B. 2 s C. 3 s D. 4 s
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点
 是
是 的边
的边 上的一点,过点
上的一点,过点 作
作 ,
, ,
, ,
, 为垂足,再过点
为垂足,再过点 作
作 ,交
,交 于点
于点 ,且
,且 .
.
(1)求证:
 ;
;(2)求证:
 垂直平分
垂直平分 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,等边
 .
.(1)如图(1),若
 ,现有两点
,现有两点 、
、 分别从点
分别从点 、点
、点 同时出发,沿三角形的边顺时针运动,已知点
同时出发,沿三角形的边顺时针运动,已知点 的速度为
的速度为 ,点
,点 的速度为
的速度为 .当点
.当点 第一次到达
第一次到达 点时,
点时, 、
、 同时停止运动.点
同时停止运动.点 ,
, 运动______秒后,
运动______秒后, 为等腰三角形.
为等腰三角形.
(2)如图,点
 位于等边
位于等边 的内部,且
的内部,且 .将
.将 绕点
绕点 顺时针旋转
顺时针旋转 ,点
,点 的对应点为点
的对应点为点 .
.①依题意,补全图形;
②若
 ,
, ,求
,求 与
与 的面积比.
的面积比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12.在直线AC、BC上分别取一点M、N,使得△AMN≌△ABN,则CN=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( )

A. 1 m B. 2 m C. 3 m D. 6 m
-
科目: 来源: 题型:
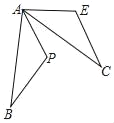
查看答案和解析>>【题目】(1)如图,△AEC绕A点顺时针旋转60°得△APB,∠PAC=20°,求∠BAE.
(2)解不等式组:
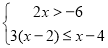
相关试题

