Question

【题目】八年级(1)班同学上数学活动课,利用角尺平分一个角(如图).设计了如下方案:

(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与M,N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.

(Ⅱ)∠AOB是一个任意角,在边OA,OB上分别取OM=ON,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与M,N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.

(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由.

(2)在方案(Ⅰ)PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.

Answer 1

【答案】(1)方案(Ⅰ)不可行.缺少证明三角形全等的条件；当∠AOB是直角时,此方案可行.

【解析】

（1）方案(Ⅰ)中判定并不能判断就是的角平分线，关键是缺少的条件，只有“边边”的条件；

（2）可行.此时和都是直角三角形，可以利用证明它们全等，然后利用全等三角形的性质即可证明为的角平分线.

(1)方案(Ⅰ)不可行.缺少证明三角形全等的条件.

∵只有OP=OP,PM=PN不能判断△OPM≌△OPN;

∴就不能判定OP就是∠AOB的平分线.

方案(Ⅱ)可行.证明:在△OPM和△OPN中,

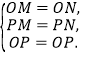
∴△OPM≌△OPN(SSS),∴∠AOP=∠BOP.

(2)当∠AOB是直角时,此方案可行.

∵PM⊥OA,PN⊥OB,

∴∠OMP=∠ONP=90°.

∵∠MPN=90°,

∴∠AOB=360°―∠OMP―∠ONP―∠MPN=90°.

∵PM⊥OA,PN⊥OB,且PM=PN,

∴OP为∠AOB的平分线(到角两边距离相等的点在这个角的平分线上).

当∠AOB不为直角时,此方案不可行.