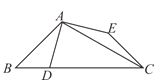
【题目】如图,△ABC中,∠ABC=45°,∠BCA=30°,点D在BC上,点E在△ABC外,且AD=AE=CE,AD⊥AE,则![]() 的值为____________.
的值为____________.
参考答案:
【答案】![]()
【解析】
过A点作BC的垂线,E点作AC的垂线,构造全等三角形,利用对应角相等计算得出∠DAM=15°,在AM上截取AG=DG,则∠DGM=30°,设DM=a,通过勾股定理可得到DG=AG=2a,GM=![]() a,AM=BM=(
a,AM=BM=(![]() ,BD=(
,BD=(![]() ,AB=
,AB=![]() (
(![]() ,代入计算即可.
,代入计算即可.
过A点作AM⊥BC于M点,过E点EN⊥AC于N点.
∵∠BCA=30°,AE=EC
∴AM=![]() AC,AN=
AC,AN=![]() AC
AC
∴AM=AN
又∵AD=AE
∴RtADM RtAEN(HL)
∴∠DAM=∠EAN
又∵∠MAC=60°,AD⊥AE
∴∠DAM=∠EAN=15°
在AM上截取AG=DG,则∠DGM=30°
设DM=a,则 DG=AG=2a,
根据勾股定理得:GM=![]() a,
a,
∵∠ABC=45°
∴AM=BM=(![]()
∴BD=(![]() ,AB=
,AB=![]() (
(![]() ,
,
∴![]()
故答案为:![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(其中∠P=30°)的直角顶点放在点O处,一边OQ在射线OA上,另一边OP与OC都在直线AB的上方.将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.
(1)如图2,经过t秒后,OP恰好平分∠BOC.
①求t的值;
②此时OQ是否平分∠AOC?请说明理由;
(2)若在三角板转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠POQ?请说明理由;
(3)在(2)问的基础上,经过多少秒OC平分∠POB?(直接写出结果).

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明箱子中有2个红球,1个黑球和1个白球,四个小球的形状、大小完全相同.
(1)从中随机摸取1个球,则摸到黑球的概率为 ;
(2)小明和小贝做摸球游戏,游戏规则如下.

你认为这个游戏公平吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c,ab<0,ac>0,且|c|>|b|>|a|,数轴上a,b,c对应的点分别为A,B,C.
(1)若a=1,请你在数轴上标出点A,B,C的大致位置;
(2)若|a|=﹣a,则a 0,b 0,c 0;(填“>”、“<“或“=”)
(3)小明判断|a﹣b|﹣|b+c|+|c﹣a|的值一定是正数,小明的判断是否正确?请说明理由.
-
科目: 来源: 题型:
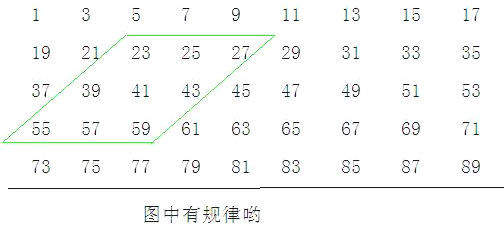
查看答案和解析>>【题目】下图的数阵是由全体奇数排成:
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;
(3)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC=CD=AD=4,∠DAB=∠B=∠C=∠D=90°,E,F分别是边BC,CD上的点,且CE=
 BC,F为CD的中点,问△AEF是什么三角形?请说明理由.
BC,F为CD的中点,问△AEF是什么三角形?请说明理由.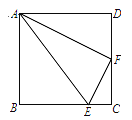
-
科目: 来源: 题型:
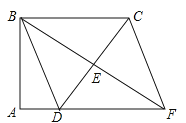
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.
(1)求证:四边形BDFC是平行四边形;
(2)若CB=CD,求四边形BDFC的面积.
相关试题

