搜索
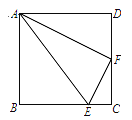
【题目】如图，在四边形ABCD中，AB＝BC＝CD＝AD＝4，∠DAB＝∠B＝∠C＝∠D＝90°，E，F分别是边BC，CD上的点，且CE＝
BC，F为CD的中点，问△AEF是什么三角形？请说明理由.
参考答案：
【答案】直角三角形,理由见解析
【解析】
根据CE＝
BC，F为CD的中点，求出CE、CF、DF、BE的长，利用勾股定理求出EF2、AF2、AE2的长，利用勾股定理的逆定理判定即可.
∵AB＝BC＝CD＝AD＝4，CE＝BC，F为CD的中点
∴CE=1,CF=DF=2,BE=3
又∵∠DAB＝∠B＝∠C＝∠D＝90°
∴EF2=CE2+CF2=12+22=5 ,AF2=AD2+DF2=22+42=20 ,AE2=AB2+BE2=42+32=25
∵EF2+ AF2=5+20=25 =AE2
∴△AEF是直角三角形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有理数a，b，c，ab＜0，ac＞0，且|c|＞|b|＞|a|，数轴上a，b，c对应的点分别为A，B，C．
（1）若a=1，请你在数轴上标出点A，B，C的大致位置；
（2）若|a|=﹣a，则a 0，b 0，c 0；（填“＞”、“＜“或“=”）
（3）小明判断|a﹣b|﹣|b+c|+|c﹣a|的值一定是正数，小明的判断是否正确？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠ABC＝45°，∠BCA＝30°，点D在BC上，点E在△ABC外，且AD＝AE＝CE，AD⊥AE，则
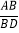的值为____________．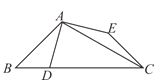
-
科目： 来源： 题型：
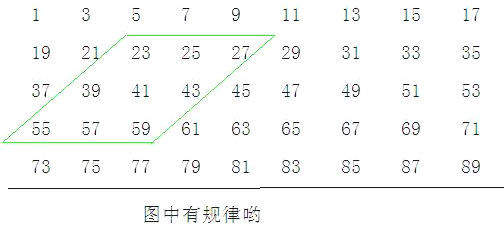
查看答案和解析>>【题目】下图的数阵是由全体奇数排成：
（1）图中平行四边形框内的九个数之和与中间的数有什么关系？
（2）在数阵图中任意作一类似（1）中的平行四边形框，这九个数之和还有这种规律吗？请说出理由；
（3）这九个数之和能等于1998吗？2005，1017呢？若能，请写出这九个数中最小的一个；若不能，请说出理由．
-
科目： 来源： 题型：
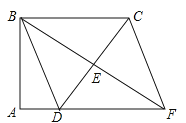
查看答案和解析>>【题目】如图，在四边形ABCD中，∠A＝∠ABC＝90°，AD＝1，BC＝3，点E是边CD的中点，连接BE并延长交AD的延长线于点F，连接CF．
(1)求证：四边形BDFC是平行四边形；
(2)若CB＝CD，求四边形BDFC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图各图是棱长为1cm的小正方体摆成的，如图①中,从正面看有1个正方形，表面积为6cm2；如图②中,从正面看有3个正方形，表面积为18cm2；如图③，从正面看有6个正方形，表面积为36cm2；…
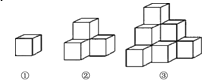
(1)第6个图中，从正面看有多少个正方形?表面积是多少?
(2)第n个图形中，从正面看有多少个正方形?表面积是多少?
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂有甲、乙两台机器加工同一种零件，已知一小时甲加工的零件数与一小时乙加工的零件数的和为36个，甲加工80个零件与乙加工100个零件的所用时间相等．求甲、乙两台机器每小时分别加工零件多少个？
相关试题
