【题目】有理数a,b,c,ab<0,ac>0,且|c|>|b|>|a|,数轴上a,b,c对应的点分别为A,B,C.
(1)若a=1,请你在数轴上标出点A,B,C的大致位置;
(2)若|a|=﹣a,则a 0,b 0,c 0;(填“>”、“<“或“=”)
(3)小明判断|a﹣b|﹣|b+c|+|c﹣a|的值一定是正数,小明的判断是否正确?请说明理由.
参考答案:
【答案】(1)在数轴上标出点A,B,C的大致位置如图见解析;(2)<,>,<;(3)小明的判断正确.理由见解析.
【解析】
(1)a=1时,易得b<0,c>0,再利用|c|>|b|>|a|得到c>1,-c<b<-1,然后在数轴上大致标出数b、c即可;
(2)根据绝对值的意义得到a<0,则由ab<0,ac>0易得b>0,c<0;
(3)讨论:当a>0时,则b<0,c>0,再由|c|>|b|>|a|得到a-b>0,b+c>0,c-a>0,然后根据绝对值的意义去绝对值合并得到原式=-2b,从而得到原式的值为正数;当a<0时,同样方法得到原式的值为正数,于是判断|a-b|-|b+c|+|c-a|的值一定是正数.
(1)a=1时,b<0,c>0,
而|c|>|b|>|a|,
所以c>1,﹣c<b<﹣1,
如图,
![]()
(2)∵|a|=﹣a,
∴a<0,
∴b>0,c<0,
故答案为<,>,<;
(3)小明的判断正确.理由如下:
当a>0时,则b<0,c>0,
而|c|>|b|>|a|,
则|a﹣b|﹣|b+c|+|c﹣a|=a﹣b﹣(b+c)+c﹣a=﹣2b>0;
当a<0时,则b>0,c<0,
而|c|>|b|>|a|,
则|a﹣b|﹣|b+c|+|c﹣a|=﹣(a﹣b)+(b+c)+a﹣c=2b>0;
综上所述,|a﹣b|﹣|b+c|+|c﹣a|的值一定是正数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知把直线y=kx+b(k≠0)沿着y轴向上平移3个单位后,得到直线y=﹣2x+5.
(1)求直线y=kx+b(k≠0)的解析式;
(2)求直线y=kx+b(k≠0)与坐标轴围成的三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CE∥BF,CE=BF.则添加下列条件还不能使△EAC≌△FDB.( )

A. AB=CDB. AE∥DFC. ∠E=∠FD. AE=DF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中直线表示三条相互交叉的路,现要建一个货运中转站,要求它到三条公路的距离相等,则选择的地址有( )

A. 4处B. 3处C. 2处D. 1处
-
科目: 来源: 题型:
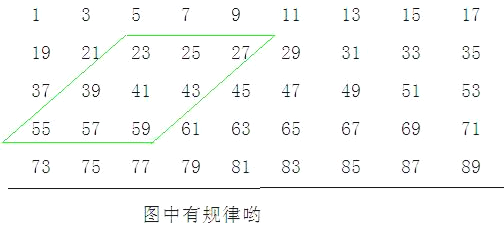
查看答案和解析>>【题目】下图的数阵是由全体奇数排成:
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;
(3)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.
-
科目: 来源: 题型:
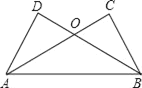
查看答案和解析>>【题目】如图,AC⊥BC,AD⊥DB,下列条件中: ①∠ABD=∠BAC;②∠DAB=∠CBA;③AD=BC;④∠DAC=∠CBD,能使△ABC≌△BAD的有_____(把所有正确结论的序号都填在横线上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图各图是棱长为1cm的小正方体摆成的,如图①中,从正面看有1个正方形,表面积为6cm2;如图②中,从正面看有3个正方形,表面积为18cm2;如图③,从正面看有6个正方形,表面积为36cm2;…
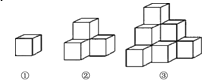
(1)第6个图中,从正面看有多少个正方形?表面积是多少?
(2)第n个图形中,从正面看有多少个正方形?表面积是多少?
相关试题

