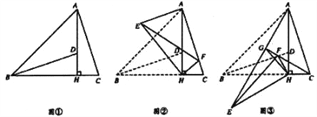
【题目】如图①,△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,且DH=CH,连接BD.(1)求证:BD=AC;
(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE.
ⅰ)如图②,当点F落在AC上时(F不与C重合),若BC=4,tanC=3,求AE的长;
ⅱ)如图③,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由。
参考答案:
【答案】(1)证明见解析;(2)(I)AE=![]() ;(II)
;(II) ![]() .
.
【解析】(1)先判断出AH=BH,再判断出△BHD≌△AHC即可;
(2)①先根据tanC=3,求出AH=3,CH=1,然后根据△EHA≌△FHC,得到,HP=3AP,AE=2AP,最后用勾股定理即可;
②先判断出△AGQ∽△CHQ,得到![]() ,然后判断出△AQC∽△GQH,用相似比即可.
,然后判断出△AQC∽△GQH,用相似比即可.
解:(1)在Rt△AHB中,∠ABC=45°,
∴AH=BH,
在△BHD和△AHC中,
AH=BH,∠BHD=∠AHC=90°,DH=CH,
∴△BHD≌△AHC,
∴BD=AC,
(2)①如图,
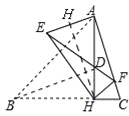
在Rt△AHC中,
∵tanC=3,∴![]() =3,
=3,
设CH=x,∴BH=AH=3x,
∵BC=4,∴3x+x=4,∴x=1,
∴AH=3,CH=1,
由旋转知,∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH,
∴∠EHA=∠FHC, ![]() ,
,
∴△EHA≌△FHC,
∴∠EAH=∠C,
∴tan∠EAH=tanC=3,
过点H作HP⊥AE,
∴HP=3AP,AE=2AP,
在Rt△AHP中,AP2+HP2=AH2,
∴AP2+(3AP)2=9,
∴AP=![]() ,
,
∴AE=![]() ;
;
②由①有,△AEH和△FHC都为等腰三角形,
∴∠GAH=∠HCG=90°,
∴△AGQ∽△CHQ,
∴![]() ,
,
∴![]() ,
,
∵∠AQC=∠GQE,
∴△AQC∽△GQH,
∴![]() =sin30°=
=sin30°=![]() .
.
“点睛”此题是几何变换综合题,主要考查例 旋转的性质,全等三角形的性质和判定,勾股定理,锐角三角函数的意义,等腰三角形的判定和性质,解本题的关键是相似三角形性质和判定的运用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的下列线段中将三角形的面积分成相等两部分的是( )
A. 中线 B. 角平分线
C. 高 D. 以上都对
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x2﹣2x﹣k=0没有实数根,则k的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的农历三月初一为通州风筝节.这天,小刘同学正在江海明珠广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.
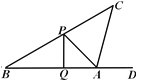
(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,试求A、B之间的距离;
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC为多少米?(结果可保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直角三角形三边扩大同样的倍数,得到的新的三角形是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 任意三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形两锐角的平分线相交得到的钝角为( )
A.150o
B.135o
C.120o
D.120o或135o -
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC的三个顶点的横坐标乘以﹣1,纵坐标不变,则所得图形( )
A. 与原图形关于y轴对称
B. 与原图形关于x轴对称
C. 与原图形关于原点对称
D. 向x轴的负方向平移了一个单位
相关试题

