【题目】二次函数![]() ,其中
,其中![]() .
.
(1)求该二次函数的对称轴方程;
(2)过动点C(0, ![]() )作直线
)作直线![]() ⊥y轴.
⊥y轴.
① 当直线![]() 与抛物线只有一个公共点时, 求
与抛物线只有一个公共点时, 求![]() 与
与![]() 的函数关系;
的函数关系;
② 若抛物线与x轴有两个交点,将抛物线在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,得到一个新的图象. 当
轴翻折,图象的其余部分保持不变,得到一个新的图象. 当![]() =7时,直线
=7时,直线![]() 与新的图象恰好有三个公共点,求此时
与新的图象恰好有三个公共点,求此时![]() 的值;
的值;
(3)若对于每一个给定的x的值,它所对应的函数值都不小于1,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ,②
,②![]() ;(3)
;(3)![]()
【解析】试题分析:(1)代入对称轴方程即可求解;
(2)①直线l与抛物线只有一个公共点,则顶点的纵坐标是n,即可得到m、n的关系;
② 依题可知:当![]() 时,直线
时,直线![]() 与新的图象恰好有三个公共点,从而可求出m的值;
与新的图象恰好有三个公共点,从而可求出m的值;
(3)先求出抛物线的顶点坐标,根据题意得出不等式组,求解即可.
试题解析:(1)对称轴方程: ![]() .
.
(2)①∵直线![]() 与抛物线只有一个公共点,
与抛物线只有一个公共点,
∴![]() .
.
② 依题可知:当![]() 时,直线
时,直线![]() 与新的图象恰好有三个公共点.
与新的图象恰好有三个公共点.
∴![]() .
.
(3)抛物线![]() 的顶点坐标是
的顶点坐标是![]() .
.
依题可得 ![]()
解得![]()
∴ m的取值范围是![]() .
.
-
科目: 来源: 题型:
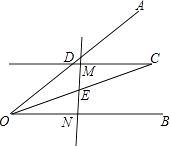
查看答案和解析>>【题目】如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,4),(﹣1,2).

(1)①请在如图所示的网格平面内作出平面直角坐标系;
②将△ABC向右平移2个单位长度,然后再向下平移3个单位长度,得到△A′B′C′,画出平移后的△A′B′C′.
(2)写出点△A′B′C′各个顶点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2+7x=12的一般形式:______________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在平面直角坐标系中的位置如图所示.

(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出△A1B1C1各顶点坐标;
(2)将△ABC向左平移1个单位,作出平移后的△A2B2C2 , 并写出△A2B2C2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品原价800元,连续两次降价a%后售价为578元,下列所列方程正确的是( )
A.800(1+a%)2=578
B.800(1﹣a%)2=578
C.800(1﹣2a%)=578
D.800(1﹣a2%)=578 -
科目: 来源: 题型:
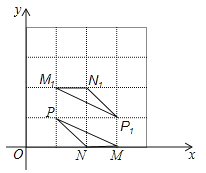
查看答案和解析>>【题目】在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1是关于某一点中心对称,则对称中心的坐标为 .
相关试题

