【题目】在平面直角坐标系![]() 中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于
中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于![]() 轴的对称点为B′,点C关于
轴的对称点为B′,点C关于![]() 轴的对称点为C′.
轴的对称点为C′.
(1)A′的坐标为 ,B′的坐标为 ,C′的坐标为 .
(2)建立平面直角坐标系,描出以下三点A、B′、C′,并求△AB′C′的面积.
参考答案:
【答案】(1)(1,-5),(4,-2)、(1,0);(2)图详见解析,7.5 .
【解析】
(1)关于原点对称的两点的横、纵坐标都是互为相反数;关于x轴对称的两点的横坐标相同,纵坐标互为相反数;关于y轴对称的两点的横坐标互为相反数,纵坐标相同;
(2)根据点A′(1,-5),B′(4,-2),C′(1,0)在平面直角坐标系中的位置,可以求得A′C′=5,B′D=3,所以由三角形的面积公式进行解答.
解:(1)∵A(-1,5),
∴点A关于原点O的对称点A′的坐标为(1,-5).
∵B(4,2),
∴点B关于x轴的对称点B′的坐标为(4,-2).
∵C(-1,0),
∴点C关于y轴的对称点C′的坐标为(1,0).
故答案为:(1,-5),(4,-2),(1,0).
(2)如图,
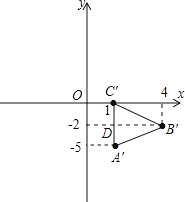
∵A′(1,-5),B′(4,-2),C′(1,0).
∴A′C′=|-5-0|=5,B′D=|4-1|=3,
![]() ,即△A′B′C′的面积是7.5.
,即△A′B′C′的面积是7.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 是
是 的中点,
的中点, 是
是 的中点,过点
的中点,过点 作
作 交
交 的延长线于点
的延长线于点 .
.
(1)求证:
 ;
;(2)求证:四边形
 是菱形;
是菱形;(3)若
 ,
, ,求菱形
,求菱形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=5,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,则下列结论中错误的是( )

A.BE=4
B.∠F=30°
C.AB∥DE
D.DF=5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1 , △AB1C的面积为S2 , 则S1 , S2的大小关系为( )

A.S1>S2
B.S1=S2
C.S1<S2
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学学生为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.

请根据图中提供的信息,解答下面的问题:
(1)参加调查的学生共有 人,在扇形图中,表示“其他球类”的扇形的圆心角为 度;
(2)将条形图补充完整;
(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有多少人呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点
 、
、 ,连接
,连接 .如果点
.如果点 在直线
在直线 上,且点
上,且点 到直线
到直线 的距离不大于1,那么称点
的距离不大于1,那么称点 是线段
是线段 的“临近点”.
的“临近点”.
(1)判断点
 是否是线段
是否是线段 的“临近点”,并说明理由;
的“临近点”,并说明理由;(2)若点
 是线段
是线段 的“临近点”.①求
的“临近点”.①求 的取值范围;②设直线
的取值范围;②设直线 与
与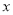 轴交于
轴交于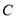 点,试用
点,试用 表达
表达 的面积
的面积 ,并求出
,并求出 的最大面积.
的最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学新建了一栋7层的教学大楼,每层楼有8间教室,进出这栋大楼共有八道门,其中四道正门大小相同,四道侧门大小也相同.安全检查中,对八道门进行了测试:当同时开启一道正门和两道侧门时,2分内可以通过560名学生;当同时开启一道正门和一道侧门时,4分内可以通过800名学生.
(1)平均每分内一道正门和一道侧门分别可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低30%.安全检查规定:在紧急情况下全大楼的学生应在5分内通过这八道门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问建造的这八道门是否符合安全规定?请说明理由.
相关试题

