搜索
【题目】如图，四边形ABCD中，E、F、G、H依次是各边中点，O是四边形内一点，若S四边形AEOH=3，S四边形BFOE=4，S四边形CGOF=5，则S四边形DHOG= ． 
参考答案：
【答案】4
【解析】解：连接OC，OB，OA，OD，
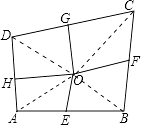
∵E、F、G、H依次是各边中点，
∴△AOE和△BOE等底等高，所以S△OAE=S△OBE，
同理可证，S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE，
∵S四边形AEOH=3，S四边形BFOE=4，S四边形CGOF=5，
∴3+5=4+S四边形DHOG，
解得，S四边形DHOG=4．
故应填4．
【考点精析】掌握三角形的面积是解答本题的根本，需要知道三角形的面积=1/2×底×高．
-
科目： 来源： 题型：
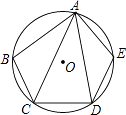
查看答案和解析>>【题目】如图，在⊙O的内接五边形ABCDE中，∠B+∠E=215°，则∠CAD=°．
-
科目： 来源： 题型：
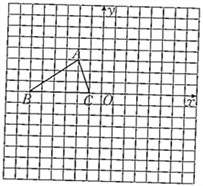
查看答案和解析>>【题目】如图，已知△ABC的三个顶点的坐标分别为A(-2，3)、B(-6，0)、C(-1，0).
(1)画出将△ABC绕坐标原点O逆时针旋转90°图形.
(2)填空：以A、B、C为顶点的平行四边形的第四个顶点D的坐标为________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，四边形 OABC 的顶点 A、C 分别在 x 轴和 y 轴上，顶点B 在第一象限，OA//CB．
（1）如图 1，若点 A(6，0)，B(4，3)，点 M 是 y 轴上一点，且 SBCM SAOM ，求点 M的坐标；
（2）如图 2，点 P 是 x 轴上点 A 左边的一点，连接 PB，∠PBC 和∠PAB 的角平分线交于点D，求证：∠ABP+2∠ADB=180°；
（3）如图 3，点 P 是 x 轴上点 A 左边的一点，点 Q 是射线 BC 上一点，连接 PB、PQ，∠ABP和∠BQP 的平分线相交于点 E，求
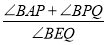的值．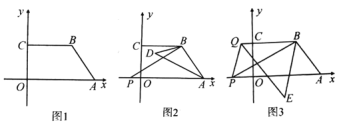
-
科目： 来源： 题型：
查看答案和解析>>【题目】推理填空：如图，E点为DF上的点，B为AC上的点，
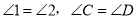，那么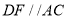
，请完成它成立的理由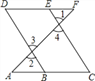
解：
______ 
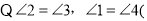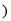
又
______ 
______ 
______ 
______ 
______ 
______ 
______ 
______ 
-
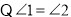
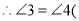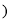
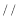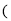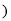
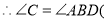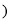
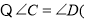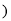
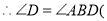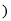
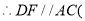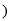
科目： 来源： 题型：
查看答案和解析>>【题目】某校为了解“课程选修”的情况，对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生（每人限报一项）进行抽样调查．下面是根据收集的数据绘制的两幅不完整的统计图．
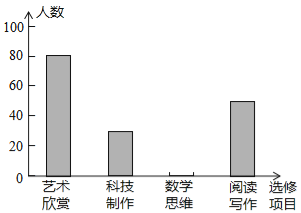
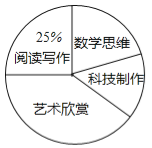
请根据图中提供的信息，解答下面的问题：
（1）此次共调查了 名学生，扇型统计图中“艺术鉴赏”部分的圆心角是 度．
（2）请把这个条形统计图补充完整．
（3）现该校共有800名学生报名参加这四个选修项目，请你估计其中有多少名学生选修“科技制作”项目．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解我校七年级
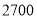名学生的体重情况，现从中随机抽取
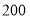名学生测量体重进行统计分析，关于本次调查下列说法正确的是（ ）A.本次调查中的总体是七年级
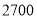名学生B.本次调查中的样本是随机抽取的
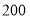名学生的体重C.本次调查中的样本容量是
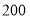名D.本次调查中的个体是七年级的每个学生
相关试题
