【题目】某种袋装奶粉标明净含量为400 g,抽检其中8袋。记录如下:
编 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
差值/g | -4.5 | +5 | 0 | +3 | 0 | 0 | +2 | -5 |
(1)净含量最大的编号为 ,净含量最小的编号为 ;
(2)这8袋抽检奶粉的总净含量是多少?
参考答案:
【答案】(1)2,8;(2)这8袋抽检奶粉的总净含量是3200.5 g.
【解析】试题分析:(1)根据正数大于零,零大于负数,可得答案;
(2)根据有理数的加法,可得答案.
试题解析:(1)5>3>2>0>4.5>5,
净含量最大的编号为2,净含量最小的编号为8,
故答案为:2,8;
(2)400×8+(4.5+5+0+3+0+0+25)=3200.5g
答:这8袋抽检奶粉的总净含量是3200.5g.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.
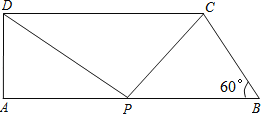
(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由.
-
科目: 来源: 题型:
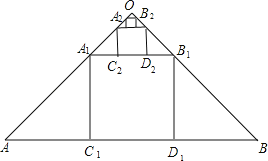
查看答案和解析>>【题目】如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3;…;依次作下去,则第n个正方形AnBnCnDn的边长是( )
A.
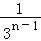 B.
B.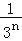 C.
C.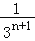 D.
D.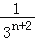
-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题
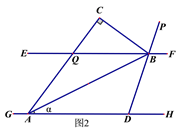
如图,直线EF∥GH,点B、A分别在直线EF、GH上,连接AB,在AB左侧作△ABC,其中∠ACB=90°,且∠DAB=∠BAC,直线BD平分∠FBC交直线GH于D.
(1)若点C恰在EF上,如图1,则∠DBA=______.
(2)将A点向左移动,其它条件不变,如图2,设∠BAD=α.
①试求∠EBC和∠PBC的大小(用α表示).
②问∠DBA的大小是否发生改变?若不变,求∠DBA的值;若变化,说明理由.
(3)若将题目条件“∠ACB=90°”,改为:“∠ACB=β”,其它条件不变,那么∠DBA= ______.(直接写出结果,不必证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】 下列命题:①直角三角形两锐角互余;②全等三角形的对应角相等;③两直线平行,同位角相等:④对角线互相平分的四边形是平行四边形.其中逆命题是真命题的个数是( )
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有3个黑球和1个白球,每个球除颜色外都相同,从中任意摸出2个球,下列事件中,不可能事件是( )
A.摸出的2个球有一个是白球
B.摸出的2个球都是黑球
C.摸出的2个球有一个黑球
D.摸出的2个球都是白球 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-3a2(ab)2
(2)x(y-5)+y(3-x)
(3)(x+2)(x-1)-3x(x+1)
相关试题

