【题目】已知反比例函数y=![]() 的图象的一支位于第一象限,点A(x1,y1),B(x2,y2)都在该函数的图象上.
的图象的一支位于第一象限,点A(x1,y1),B(x2,y2)都在该函数的图象上.
(1)m的取值范围是 ,函数图象的另一支位于第一象限,若x1>x2,y1>y2,则点B在第 象限;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点C与点A关于x轴对称,若△OAC的面积为6,求m的值.

参考答案:
【答案】(1)m>3,三;(2)9.
【解析】
(1)根据反比例函数的图象是双曲线.当k>0时,则图象在一、三象限,且双曲线是关于原点对称的;
(2)由对称性得到△OAC的面积为5.设A(x,![]() ),则利用三角形的面积公式得到关于m的方程,借助于方程来求m的值.
),则利用三角形的面积公式得到关于m的方程,借助于方程来求m的值.
(1)根据反比例函数的图象关于原点对称知,该函数图象的另一支在第三象限,且m﹣3>0,则m>3;
故答案是:m>3,三;
(2)∵点A在第一象限,且与点C关于x轴对称
∴AC⊥x轴,AC=2y=2×![]() ,
,
∴S△OAC=![]() ACx=
ACx=![]() ×2×
×2×![]() x=m﹣3,
x=m﹣3,
∵△OAC的面积为6,
∴m﹣3=6,
解得m=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△PQN中,若∠P=
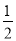 ∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.(1)已知△ABC是等边三角形,判断△ABC是否为“差角三角形”,并说明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判断△ABC是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=
 (x>0)的图象经过顶点B,则反比例函数的表达式为( )
(x>0)的图象经过顶点B,则反比例函数的表达式为( )
A. y=
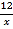 B. y=
B. y=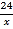 C. y=
C. y=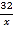 D. y=
D. y=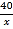
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求
 的值.
的值.(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的
 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值. -
科目: 来源: 题型:
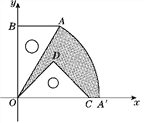
查看答案和解析>>【题目】如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把这两块三角板放置在平面直角坐标系中,且OB=3
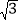 .
.(1)若某反比例函数的图象的一个分支恰好经过点A,求这个反比例函数的解析式;
(2)若把含30°角的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好落在x轴上,点A落在点A′处,试求图中阴影部分的面积.(结果保留π)
【答案】(1)反比例函数的解析式为y=
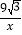 ;(2)S阴影=6π-
;(2)S阴影=6π-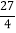 .
.【解析】分析:(1)根据tan30°=
 ,求出AB,进而求出OA,得出A的坐标,设过A的双曲线的解析式是y=
,求出AB,进而求出OA,得出A的坐标,设过A的双曲线的解析式是y=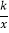 ,把A的坐标代入求出即可;(2)求出∠AOA′,根据扇形的面积公式求出扇形AOA′的面积,求出OD、DC长,求出△ODC的面积,相减即可求出答案.
,把A的坐标代入求出即可;(2)求出∠AOA′,根据扇形的面积公式求出扇形AOA′的面积,求出OD、DC长,求出△ODC的面积,相减即可求出答案.本题解析:
(1)在Rt△OBA中,∠AOB=30°,OB=3
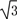 ,
,∴AB=OB·tan 30°=3.
∴点A的坐标为(3,3
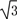 ).
).设反比例函数的解析式为y=
 (k≠0),
(k≠0),∴3
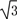 =
= ,∴k=9
,∴k=9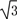 ,则这个反比例函数的解析式为y=
,则这个反比例函数的解析式为y=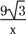 .
.(2)在Rt△OBA中,∠AOB=30°,AB=3,
sin ∠AOB=
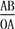 ,即sin 30°=
,即sin 30°=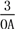 ,
,∴OA=6.
由题意得:∠AOC=60°,S扇形AOA′=
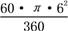 =6π.
=6π.在Rt△OCD中,∠DOC=45°,OC=OB=3
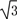 ,
,∴OD=OC·cos 45°=3
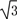 ×
×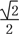 =
=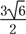 .
.∴S△ODC=
 OD2=
OD2=
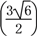 =
= .
.∴S阴影=S扇形AOA′-S△ODC=6π-
 .
.点睛:本题考查了勾股定理、待定系数法求函数解析式、特殊角的三角函数值、扇形的面积及等腰三角形的性质,本题属于中档题,难度不大,将不规则的图形的面积表示成多个规则图形的面积之和是解答本题的关键.
【题型】解答题
【结束】
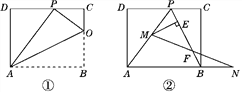
26【题目】矩形ABCD一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.
(1)如图①,已知折痕与边BC交于点O,连接AP,OP,OA.
① 求证:△OCP∽△PDA;
② 若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)如图②,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P,A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M,N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2+6x+5=0 (配方法)
(2)x2﹣1=2(x+1)(因式分解法)
(3)2x2+3=6x (公式法)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于 x 的方程 2x2+kx﹣1=0.
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是﹣1,求另一个根及 k 值.
相关试题

