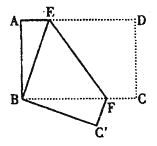
【题目】如图,长方形纸片ABCD,AD∥BC,将长方形纸片折叠,使点D与点B重合,点C落在点C'处,折痕为EF,
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE的度数.
(3)若AB=6,AD=8,求AE的长.
参考答案:
【答案】(1)、证明过程见解析;(2)、54°;(3)、![]() .
.
【解析】试题分析:(1)、根据折叠图形得出∠DEF=∠BEF,根据AD∥BC得出∠DEF=∠EFB,从而得到答案;(2)、根据等腰三角形的性质进行求解;(3)、根据Rt△ABE的勾股定理求出答案.
试题解析:(1)、∵折叠 ∴∠DEF=∠BEF 又∵AD∥BC ∴∠DEF=∠EFB ∴∠BEF=∠EFB ∴BE=BF
(2)、∵∠ABC=90° ∴∠EBF=90°-18°=72° ∴∠EBF=![]() =54°
=54°
(3)、设AE=x,则ED=BE=8-x ∴在Rt△ABE中 x2+62=(8-x)2 ∴x=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.
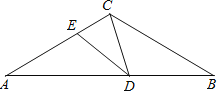
(1)当DE∥BC时,△ACD的形状按角分类是直角三角形;
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),回答下列问题(直接写出结果):
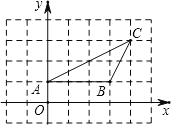
(1)点A关于原点对称的点的坐标为
(2)点C关于y轴对称的点的坐标为
(3)若△ABD与△ABC全等,则点D的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)x2-4x
(2)﹣2x2﹢2
(3)4x5-4x4+x3
(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
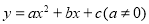 的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣4).
的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣4).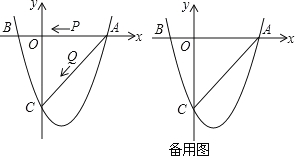
(1)求该二次函数的解析;
(2)若点P、Q同时从A点出发,以每秒1个单位长度的速度分别沿AB、AC边运动,其中一点到达端点时,另一点也随之停止运动.
①当点P运动到B点时,在x轴上是否存在点E,使得以A、E、Q为顶点的三角形为等腰三角形?若存在,请求出E点的坐标;若不存在,请说明理由.
②当P、Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请直接写出t的值及D点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点M(-2,1)关于x轴对称点N的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个四边形的边长依次为a、b、c、d,且a2+b2+c2+d2﹣2ac﹣2bd=0,则这个四边形的性状是
相关试题

