【题目】如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.
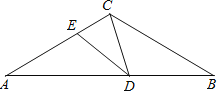
(1)当DE∥BC时,△ACD的形状按角分类是直角三角形;
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
参考答案:
【答案】(1)、直角三角形;(2)、△ECD可以是等腰三角形,∠AED=60°或105°
【解析】
试题分析:(1)、由DE∥BC得到∠BCD=∠CDE=30°,再由∠ACB=120°,得到∠ACD=120°﹣30°=90°,则△ACD是直角三角形;(2)、分类讨论:当∠CDE=∠ECD时,EC=DE;当∠ECD=∠CED时,CD=DE;当∠CED=∠CDE时,EC=CD;然后利用等腰三角形的性质和三角形的内角和定理进行计算.
试题解析:(1)、∵△ABC中,AC=BC, ∴∠A=∠B=![]() =
=![]() =30°,
=30°,
∵DE∥BC, ∴∠ADE=∠B=30°, 又∵∠CDE=30°, ∴∠ADC=∠ADE+∠CDE=30°+30°=60°,
∴∠ACD=180°﹣∠A﹣∠ADC=180°﹣30°﹣60°=90°, ∴△ACD是直角三角形;
(2)、△ECD可以是等腰三角形.理由如下:
①当∠CDE=∠ECD时,EC=DE, ∴∠ECD=∠CDE=30°, ∵∠AED=∠ECD+∠CDE, ∴∠AED=60°,
②当∠ECD=∠CED时,CD=DE, ∵∠ECD+∠CED+∠CDE=180°,
∴∠CED=![]() =
=![]() =75°, ∴∠AED=180°﹣∠CED=105°,
=75°, ∴∠AED=180°﹣∠CED=105°,
③当∠CED=∠CDE时,EC=CD, ∠ACD=180°﹣∠CED﹣∠CDE=180°﹣30°﹣30°=120°,
∵∠ACB=120°, ∴此时,点D与点B重合,不合题意.
综上,△ECD可以是等腰三角形,此时∠AED的度数为60°或105°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,与表示数-2的点的距离为3个单位长度的点所表示的数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(a+1,b﹣2)在第二象限,则点B(﹣a,b+1)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列因式分解错误的是( )
A. 2ax-a=a(2x-1)B. x2-2x+1=(x-1)2
C. 4ax2-a=a(2x-1)2D. ax2+2ax-3a=a(x-1)(x+3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),回答下列问题(直接写出结果):
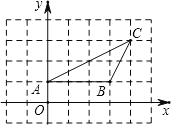
(1)点A关于原点对称的点的坐标为
(2)点C关于y轴对称的点的坐标为
(3)若△ABD与△ABC全等,则点D的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)x2-4x
(2)﹣2x2﹢2
(3)4x5-4x4+x3
(4)

-
科目: 来源: 题型:
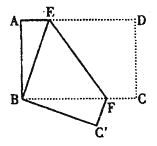
查看答案和解析>>【题目】如图,长方形纸片ABCD,AD∥BC,将长方形纸片折叠,使点D与点B重合,点C落在点C'处,折痕为EF,
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE的度数.
(3)若AB=6,AD=8,求AE的长.
相关试题

